Унарная позиционная и непозиционная система счисления чем они различаются и привести примеры
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления.
Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
Ответ
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации.
К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.
В непозиционных системах счисления величина, обозначающая цифру, не зависит от положения в числе. К тому же, система может накладывать ограничения на расстановку цифр, например, чтобы цифры располагались по убыванию.
Унарная система счисления – это система счисления, в которой для записи чисел используется только один знак – 1 («палочка»). Следующее число получается из предыдущего добавлением новой 1; их количество (сумма) равно самому числу.
Именно такая система применяется для начального обучения счету детей (можно вспомнить «счетные палочки»).
Другими словами, использование именно унарной системы оказывается важным педагогическим приемом для введения детей в мир чисел и действий с ними.
Система счисления
Содержание:
Задумывались ли вы над тем, почему при сложении тех или иных чисел получается строго определённое число? А почему мы обходимся всего десятью цифрами? Странные вопросы. Дело в том, что мы привыкли проводить вычисления, используя всего одну и ту же систему счисления. Однако это было так не всегда.
Системой счисления принято называть знаковую систему, в которой были приняты определённые правила записи чисел. Знаки, с помощью которых записывают числа, мы называем цифрами, а их совокупность — алфавитом системы счисления.
Для любой системы счисления, цифры которые служат для обозначения чисел, называемые узловыми; остальные числа (алгоритмические) получаются в результате операций над узловыми числами.
В Древнем Вавилоне узловыми числами выступали 1,10,60;
Системы счисления отличаются друг от друга выбором узловых чисел и способами образования алгоритмических чисел. В информатике выделяют такие виды систем счисления, как:
Унарная система
В самой древней и простой унарной системе счисления, для записи любых чисел использовался всего лишь один символ — в виде зарубки, выемки, узелка или камушка.
Если вы думаете, что не пользуетесь этой системой счисления, тогда не считайте на пальцах!
Непозиционная система счисления
Для такой системы счисления количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Примерно в III тысячелетии до н.э. древние египтяне разработали десятичную непозиционную систему счисления, в которой для обозначения узловых чисел 1, 10, 100 использовались символы – иероглифы.
В большинстве непозиционных систем счисления новые числа образуются путём сложения узловых чисел.
Каноническим примером непозиционной системы счисления всегда приводится римская система счисления. В качестве узловых цифр здесь применялись заглавные буквы латинского алфавита:
I = 1,
V = 5,
X = 10,
L = 50,
C = 100,
D = 500,
M = 1000
Например, II = 1 + 1 = 2
здесь символ I обозначает единицу независимо от места в числе.
Однако римская система не может быть полностью непозиционной, так как меньшая цифра, которая стоящая слева перед большей, должна вычитаться из неё:
IV = 4, в то время как:
VI = 6
Непозиционной системой счисления являлась и кириллическая система счисления — система счисления, применяемая на территории Древней Руси до XVIII века, основанная на алфавитной записи чисел с использованием кириллицы.
Позиционная система счисления
В позиционной системе счисления, количественный эквивалент цифры как раз зависит от её положения в записи числа. Основание позиционной системы счисления соответствует количеству цифр, которые составляют её алфавит.
Основным примером позиционной системы счисления является десятичная система записи чисел, к которой мы все так уже привыкли с детства, и в которой производим все основные математические вычисления.
Алфавитом десятичной системы являются цифры от 0 до 9. Образование чисел в ней происходит следующим образом: значения цифр умножаются на их «веса» соответствующих разрядов, а затем все полученные значения складываются.
Числительными русского языка, такое значением хорошо отражается, к примеру: «пять-сот семь-десят два».
Основанием позиционной системы счисления является любое натуральное число q>1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0,1. q−1, каждое из которых записывается при помощи одного уникального символа; младшей цифрой всегда выступает 0.
Основными преимуществами любой позиционной системы счисления являются простота выполнения арифметических операций и небольшое количество символов, используемых в записи чисел.
Представление числа в позиционной системе счисления
В позиционной системе счисления с основанием q всякое число может быть представлено по формуле (развёрнутая форма записи):
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Свёрнутой формой записи числа называется его представление в виде:
Унарная система счисления
Здравствуйте, в этой статье пойдет речь про унарную систему счисления. Ниже мы разберем основные определения, касающиеся данной темы, историю происхождения, её достоинства и недостатки. Рассмотрим области, где применяется эта система исчисления, примеры и её значение в информатике и других прикладных науках.
Экскурс в прошлое
Как только древние люди научились подсчитывать предметы, то сразу появилась потребность в отображении чисел. Для подсчета добычи, овец или жителей племени использовались зарубки на деревьях, засечки на костях животных и стенах пещер, камушки, и другие предметы, с помощью которых можно отобразить количественное значение.
Пример У.С: засечки на кости
Ученые археологи нашли такие «записи», которые сохранились до наших дней со времен Палеолита. А это, немного немало, около десяти тысяч лет до нашей эры. Со временем люди стали объединять предметы в группы, появились более совершенные позиционные системы. Однако единичная система исчисления, еще называемая учеными унарной, никуда не ушла – человечество пользуется ей до сих пор. Рассмотрим её более подробно…
Определение и его разъяснение
Унарной – называется непозиционная система счисления, которая состоит всего лишь из одного знака (цифры), который обозначает единицу. Как было написано выше, за «знак» можно было взять всё что угодно – палочку на стене пещеры или зарубку на дереве.
Теперь немного поговорим, почему она называется непозиционной. Тут все очень просто – в таких отображениях положение знака (цифры) не влияет на его значение. Возьмите две спички и примите одну за единицу, поменяйте их местами – число не изменится, каждая спичка, как обозначала 1, так и будет её обозначать.
В позиционных исчислениях все несколько иначе. Давайте возьмем в пример, самое популярное в мире, десятичное счисление. Запишите число 10 и поменяйте нулик с единичкой местами – у вас получится другое число (01). Почему так вышло? Дело в том, что в первом случае 1 обозначала количество десятков, а во втором количество единиц. То есть, поменяв место цифры, мы изменили её значение. Поэтому представление называется позиционным. Далее рассмотрим несколько интересных фактов.
Интересные исторические факты
Не одна древняя цивилизация не использовала примитивную унарную запись в чистом виде, однако она лежала в основе большинства форм представления чисел существовавших в древности.
Преимущества и недостатки
Скорее всего, Вы сами о них уже догадались. К преимуществам унарной формы можно отнести простоту – используется всего лишь один знак, а это значит, что легко выполняются простейшие математические операции, такие как сложение и вычитание.
Недостатков же больше и они очень существенные. Именно из-за них люди предпочли использовать позиционные нумерации:
Примеры применения в мире, информатике и других науках
Заключение
Вот Вы и познакомились с самой примитивной – непозиционной унарной системой счисления. Теперь Вы знаете основные положения и примеры, касающиеся этой темы, области применения в информатике и других сферах. При возникновении вопросов задавайте их в комментариях. А также можете прочитать про Греческий формат.
Позиционные и непозиционные системы счисления



Системы счисления принято делить на два класса: непозиционные и позиционные.
В непозиционных СС от положения (позиции) цифры в записи не зависит величина, которую она обозначает. Характерным примером такой системы счисления является римская СС.
Например, в римской СС число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Например:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
Такие системы счисления используются редко, т.к. не приспособлены для вычислений.
На практике наибольшее распространение получили позиционные системы счисления.
Позиционная система счисления – система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. В каждой позиционной системе счисления имеется основание. Любое число записывается в виде последовательности из цифр основания. Количество цифр основания равно самому основанию. Основание показывает, во сколько раз вес каждой цифры меньше веса цифры, стоящей в старшем соседнем разряде.
Некоторые позиционные системы счисления
| Основание | Система счисления | Знаки |
| Двоичная | 0,1 | |
| Троичная | 0,1,2 | |
| Четвертичная | 0,1,2,3 | |
| Пятиричная | 0,1,2,3,4 | |
| Восьмиричная | 0,1,2,3,4,5,6,7 | |
| Десятиричная | 0,1,2,3,4,5,6,7,8,9 | |
| Двенадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В | |
| Шестнадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В,D,E,F |
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также называется десятичной. Называются они так потому, что каждое число можно составить из набора цифр содержащего 10 символов (цифр) –0123456789.
Возьмём, к примеру, число 246. Его запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство:
246 = 200 + 40 + 6 = 2 * 10 2 + 4 * 10 1 + 6 * 10 0
В нашем числе три цифры. Старшая цифра «2» имеет номер 3. Так вот она умножается на 10 во второй степени. Следующая цифра «4» имеет порядковый номер 2 и умножается на 10 в первой степени. Уже видно, что цифры умножаются на десять в степени на единицу меньше порядкового номера цифры.
При этом пользуются следующим алгоритмом:
1) цифра в каждой позиции умножается на основание в степени на 1 меньшую, чем номер позиции;
2) полученные таким образом значения складываются.
12310 = 1 * 10 2 + 2 * 10 1 + 3 * 10 0 ;
В других системам счисления такой перевод будет выглядеть следующим образом:
1238 = 1х8 2 + 2 х 8 1 + 3 х 8 0 = 8310;
1012 = 1 х 2 2 + 0 х 2 1 + 1 х 2 0 = 510;
1Е316 = 1 х 16 2 + 14 х 16 1 + 3 х 16 0 = 48310.
Здесь индекс числа служит указанием на основание системы счисления. Назовем основанием системы счисления число, равное мощности множества (т.е. количеству элементов множества) различных символов, допустимых в каждой позиции числа.
Десятичная система счисления является однородной. Это означает, что одних и тех же символов достаточно для изображения любого числа. Но в повседневной жизни мы пользуемся и неоднородными системами счисления, и системами счисления с другим основанием. Пример тому – неметрические системы единиц (1 пуд=40 фунтов), система счета времени (1 минута = 60 секунд).
В дальнейшем мы будем рассматривать однородные позиционные системы счисления.
Обозначим через p основание системы счисления. Тогда веса позиций числа могут быть представлены следующим образом:
Таким образом, любое число X в позиционной системе счисления с основанием p можно представить в следующей развернутой форме записи:
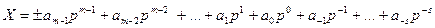
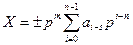
p – основание системы счисления;
m – количество позиций или разрядов, отведенное для изображения целой части числа;
s – количество разрядов, отведенное для изображения дробной части числа;
n = m + s – общее количество разрядов в числе,
ai – любой допустимый символ в разряде (т.е. должен принадлежать множеству <0,1, p-1>).
Заметим, что число, равное основанию системы счисления, в самой системе счисления записывается в виде:
В компьютерных науках наибольшее распространение получила не десятичная, а системы счисления с основанием, кратным 2 – двоичная, восьмеричная, шестнадцатеричная.
В двоичной системе счисления допустимыми символами являются только 0 и 1, а само число может быть представлено в виде последовательности нулей и единиц.
110100102 = 1 * 2 7 + 1 * 2 6 + 0 * 2 5 + 1 * 2 4 + 0 * 2 3 + 0 * 2 2 + 1 * 2 1 + 0 * 2 0 = 16210
В восьмеричной системе счисления допустимыми символами являются 0,1,…7.
2428 = 2 * 8 2 + 4 * 8 1 + 2 * 8 0 = 16210
В шестнадцатеричной системе допустимыми символами являются 0, 1, 9, A, B, C, D, E, F.
A216 = 10 * 16 1 + 2 * 16 0 = 16210
Непозиционные системы счисления
Здравствуйте, на этой странице рассмотрим одну из важных тем в информатике – а именно непозиционные системы счисления. Здесь вы узнаете, что является непозиционными системами, и познакомитесь с основными определениями, которые относятся к этой теме. Также затронем их отличия от позиционных нумераций и приведем достоинства и недостатки.
Определение непозиционной системы счисления
Непозиционными являются нумерации, где положение цифры в числе (разряд) не влияет на её значение.
Чтобы разобраться конкретно в том, что здесь написано, выберем самое популярное исчисление, которое называется десятичным. Вы все с ним знакомы. Им пользуются люди в большинстве стран мира. Алфавит десятичной нумерации состоит из арабских знаков – чисел от 0 до 9. Данный вид записи является позиционным. Почему, спросите вы? Всё просто. В качестве примера приведем два числа – 1000 и 10. Смотрите на цифру один – в зависимости от того, какое место она занимает в числе, меняется значение, которое она обозначает. В числе 1000 – тысячи, а 10 – десятки.
В непозиционных представлениях все обстоит совсем иначе. Давайте приведем в пример Римскую нотацию. Её вы тоже видели и с ней знакомы. Вспомните – в книгах по истории с помощью неё представляются века и номера монархов. Как пример, Петр I или Иван IV Грозный. Обратите внимание на I и IV, которые в арабском виде запишутся как 1 и 4. Здесь значение единицы не изменяется от того, какое место она занимает. На первом месте она стоит или на втором – неважно.
Историками считается, что исчисления, которые называются непозиционными, ведут свои корни от глубокой древности – это первые формы для счета, которые использовал человек. Поговорим дальше про их виды и разберем недостатки.
Примеры непозиционных систем счисления
Унарная непозиционная
Еще называется непозиционной единичной. Скорее всего, вы уже догадались, почему она так называется. Дело в том, что в этой форме записи используется только один знак. Это представление применяли древнейшие люди. Для записи значений использовались насечки на костях животных или стенах пещеры. Также в обиходе были зарубки на дереве. Используется до сих пор. Вспомните сериалы, где заключенные отсчитывают свои дни в неволе. Также применяется для обучения детей счету – так называемый пальцевый метод.
Унарная сс – отметки на кости
Римская непозиционная
Её мы уже привели выше. Используется до сих пор. В качестве алфавита здесь применяются латинские буквы, такие как V, I, D, M, C, X, L. Всё остальное же получается с помощью различного написания этих символов – здесь используются принципы вычитания и сложения. Так если младший разряд записывается перед старшим, то он вычитается. Если же наоборот, то складывается. Есть у неё и еще одна особенность – нет 0, который является отсутствием числа. Ниже приведена небольшая табличка с расшифровкой римских цифр.
Римское непозиционное счисление появилось в Риме на самом пике процветания империи. Однако и после того как империя распалась этим счислением пользовались еще очень долго. Она использовалась в Европе до 1200х годов, пока великий математик Леонардо Фибоначчи не издал трактат – “Книга Абака”. В нем ученый показывал превосходство позиционных систем над непозиционными.
Египетская непозиционная
Возникла в третьем тысячелетии до нашей эры. Все значения записывались здесь с помощью иероглифов. Каких-то особых правил здесь не существовало – все числовые значения просто складывались. Также не было и правил, которые относятся к записи – последовательность могла быть записана, как слева на право, так и справа налево. Иероглифы могли занимать любой разряд. Ниже приведена табличка со значениями некоторых из них.
Алфавитные системы счисления
Стоит отметить эти формы записи. Здесь все очень просто – каждой букве алфавита сопоставлялась цифра. Стоит отметить, что эти непозиционные системы являются более совершенными, чем все предыдущие, поскольку имелись обозначения десятков и сотен. К недостаткам можно отнести их сложность. Здесь можно выбрать два популярных примера.
Славянская
Использовалась нашими предками во времена древней Руси. Первые записи о ней в летописи временных лет появляются с начала десятого века. Каждой букве глаголицы соответствовало некоторое число. Полностью вышла из использования во времена Российской Империи в восемнадцатом веке, её место заняло десятичное исчисление. Пользуемся мы им, и посей день.
Греческая
Она же называется непозиционной новогреческой или ионийской. Упоминания о ней датируются третьим веком до нашей эры. Здесь счет велся буквами, которые употреблялись в римской письменности. Пришла на смену старогреческому формату. По сути, непозиционное кириллическое представление является её копией.
Достоинства и недостатки. Возможность использования в информатике и других науках.
К достоинствам можно отнести только их простоту. Как мы уже говорили выше, та же унарная непозиционная система применяется для обучения детей. Однако недостатков у них гораздо больше и они очень существенные:
Всё эти недостатки делают их использование в математике и информатике непрактичным.
Заключение
В качестве итогов можно сказать, что после прочтения этого материала вы имеете полное представление о том, что называется непозиционными системами счисления, овладели нужным определением. Знаете виды, которые использовали разные народы в различных частях земного шара. Теперь вы имеете представление о том, как считали люди в Риме, Египте, Греции и древней Руси. Знаете их плюсы и минусы. Понимаете, почему нельзя использовать их в информатике. Как по мне тема достаточно легкая, но очень интересная. При возникновении вопросов задайте их в комментариях к этой записи. Буду рад на них ответить. Также вы можете почитать другие материалы, которые затрагивают информатику на нашем сайте.