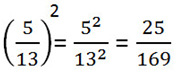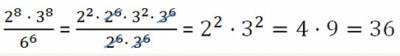Укажите чему равен показатель степени в выражении b m c ответ

Формулы степеней и корней.

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n-ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

5. Возводя степень в степень, показатели степеней перемножают:

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n-ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n-ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n, необходимо извлечь корень n–ой степени из m-ой степени этого числа а:

Формулы степеней.

6. a — n = — деление степеней;

7. — деление степеней;

8. a 1/n = ;

Источник

Степень числа

Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.

Рассмотрим умножение одинаковых чисел, например:

Произведение 5 · 5 · 5 можно записать так: 5 3 (пять в третьей степени). Выражение 5 3 — это степень. Следовательно,

Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.

Читаются степени так:

Пример. Записать в виде степени:

б) 10 · 10 · 10 · 10 = 10 4 ;

Возведение в степень

Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:

2 — это основание степени, 3 — показатель степени, 8 — степень.

a) 11 2 = 11 · 11 = 121;

б) 2 5 = 2 · 2 · 2 · 2 · 2 = 32;

в) 10 4 = 10 · 10 · 10 · 10 = 10000.

Выражения со степенями. Порядок действий

Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия. Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.

Рассмотрим два выражения:

В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.

5 2 + 2 2 = 25 + 4 = 29,

Пример 1. Найти значение выражения:

Решение: Сначала выполняется действие, заключённое в скобки:

Затем, по правилам порядка действий, выполняется возведение в степень:

И последним действием вычисляется произведение:

Пример 2. Вычислить:

Калькулятор возведения в степень

Источник

Свойства степеней. Действия со степенями

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

a — основание степени;

n — показатель степени.

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Укажите чему равен показатель степени в выражении b m c ответ

Тесты по алгебре 7 класс. Тема: «Стандартный вид одночлена»

Правильный вариант ответа отмечен знаком +

4. Какой одночлен имеет стандартный вид?

5. Из чего не состоит одночлен?

8. Какой закон используется для преобразования одночлена в стандартный вид?

d. переместительный закон умножения +

11. В каком порядке следует расположить буквенные множители?

12. Какой одночлен имеет нестандартный вид?

a. сумма всех степеней буквенных множителей +

a. приведение одночлена к его стандартному виду +

16. Какое определение у коэффициента одночлена?

b. это числовой множитель одночлена стандартного вида +

17. Коэффициенты с какими числами опускают в одночленах?

19. Как по-другому называют число 0?

a. нулевой одночлен +

тест-20. 6a 4 b 2 + 2a 4 b 2 = …

21. Как по-другому можно записать одночлен 5yz?

a. yz + yz + yz + yz + yz +

22. Как называются буквенные обозначения одночлена?

23. 4b 2 0c 6 = …

24. Какой арифметический знак опускается в одночлене?

25. Что идет первым в одночлене?

27. … × 2a 6 b = 8a 7 b

28. Какие буквенные множители используются вообще всего?

тест_30. Как будет выглядеть одночлен 8x 3 xx 5 в стандартном виде?

Источник

Каталог статей

Степень числа

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 4 6 и произносят «четыре в шестой степени».
4 • 4 • 4 • 4 • 4 • 4 = 4 6

Запись a n читается так: «а в степени n» или «n-ая степень числа a».

Выражение 0 0 (ноль в нулевой степени) считают лишённым смыслом.
• (-32) 0 = 1
• 0 234 = 0
• 1 4 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

Пример. Возвести в степень.
• 5 3 = 5 • 5 • 5 = 125
• 2.5 2 = 2.5 • 2.5 = 6.25
• (3 ) 4 = 3• 3• 3• 3 = 81
4 4 4 4 4 256

При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.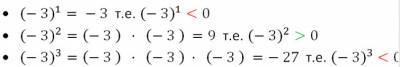

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Отрицательное число, возведённое в чётную степень, есть число положительное.

Вычислить (- 5) 4 означает найти значение четвёртой степени отрицательного числа.
(- 5) 4 = (- 5) • (- 5) • (- 5) • (- 5) = 625

Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Cвойства степени

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней

Данное свойство степеней также действует на произведение трёх и более степеней.
Примеры.
• Упростить выражение.
b • b 2 • b 3 • b 4 • b 5 = b 1+2+3+4+5 = b 15

• Представить в виде степени.
6 15 • 36 = 6 15 • 6 2 = 6 15+2 = 6 17

• Представить в виде степени.
(0,8) 3 • (0,8) 12 = (0,8) 3+12 = (0,8) 15

Свойство № 2
Частное степеней

Примеры.
• Записать частное в виде степени
(2b) 5 : (2b) 3 = (2b) 5-3 = (2b) 2

• Пример. Решить уравнение. Используем свойство частного степеней.
3 8 : t = 3 4

Свойство № 3
Возведение степени в степень

• Пример.
(a 4 ) 6 = a 4 • 6 = a 24
• Пример. Представить 3 20 в виде степени с основанием 32.
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:

Свойства 4
Степень произведения

(6 • a 2 • b 3 • c ) 2 = 6 2 • a 2 • 2 • b 3 • 2 • с 1 • 2 = 36 a 4 • b 6 • с 2

(- x 2 • y) 6 = ( (- 1) 6 • x 2 • 6 • y 1 • 6 ) = x 12 • y 6

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n • b n )= (a • b) n

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
• Пример. Вычислить.

2 4 • 5 4 = (2 • 5) 4 = 10 4 = 10 000

0,5 16 • 2 16 = (0,5 • 2) 16 = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 • 3 2 = 4 3 • 4 2 • 3 2 = 4 3 • (4 • 3) 2 = 64 • 12 2 = 64 • 144 = 9216

Пример возведения в степень десятичной дроби.
4 21 • (-0,25) 20 = 4 • 4 20 • (-0,25) 20 = 4 • (4 • (-0,25)) 20 = 4 • (- 1) 20 = 4 • 1 = 4

Свойства 5
Степень частного (дроби)

• Пример. Представить выражение в виде частного степеней.
(5 : 3) 12 = 5 12 : 3 12

Возведение в степень дроби

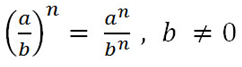
Примеры возведения в степень дроби.

Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой части, превращая смешанное число в неправильную дробь. После этого возводим в степень и числитель, и знаменатель.
Пример.

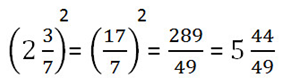
Формулу возведения в степень дроби применяют как слева направо, так и справа налево, то есть, чтобы разделить друг на друга степени одинаковыми показателями, можно разделить одно основание на другое, а показатель степени оставить неизменным.

• Пример. Найти значение выражения рациональным способом.

Источник