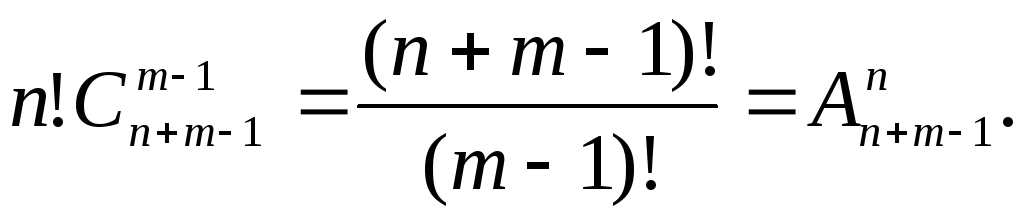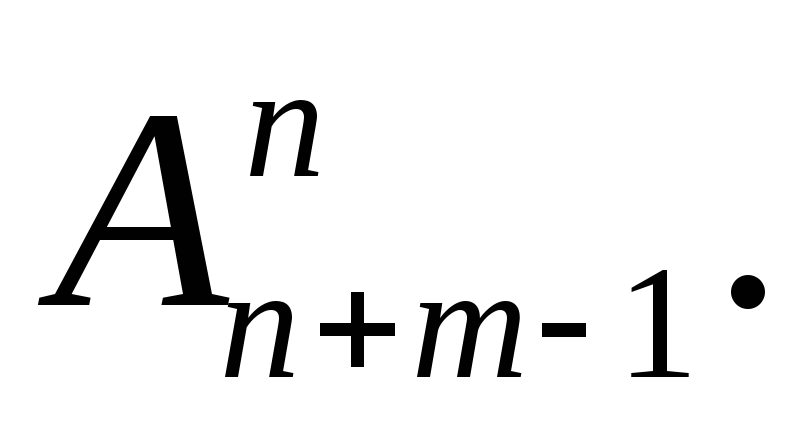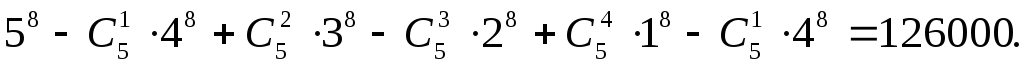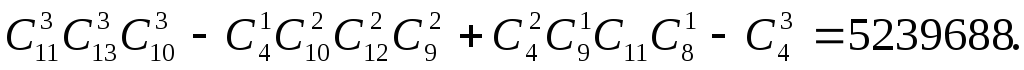сколькими способами можно надеть 5 различных колец на пальцы одной руки исключая большой палец

Сколькими способами можно надеть 5 различных колец на пальцы одной руки

Репетитор по скайпу

Задачи 51-100 с ответами

Примеры решения некоторых комбинаторных задач

Задача. Из 28 студентов группы 14 человек занимаются плаванием, 18 человек — баскетболом, 12 студентов — легкой атлетикой, 8 — плаванием и баскетболом, 7 — легкой атлетикой и баскетболом, 6 — плаванием и легкой атлетикой, 3 студентов занимаются и плаванием, и баскетболом, и легкой атлетикой. Сколько в группе студентов, которые не занимаются ни одним из данных видов спорта?

Решение.Обозначим через p − увлечение плаванием, через b − увлечение баскетболом, через a − увлечение легкой атлетикой. Подсчитаем, сколько студентов в данной группе не занимаются ни одним из данных видов спорта, то есть найдем чему равно N().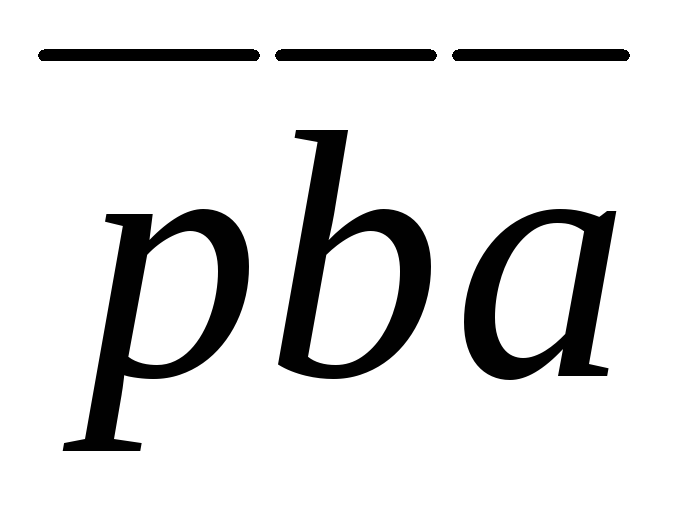

По условию задачи имеем N(p)=14, N(b)=18, N(a)=12, N(pb)=8, N(ba)=7, N(pa)=6, N(pba)=3.

Значит, по формуле включений и исключений получаем, что N(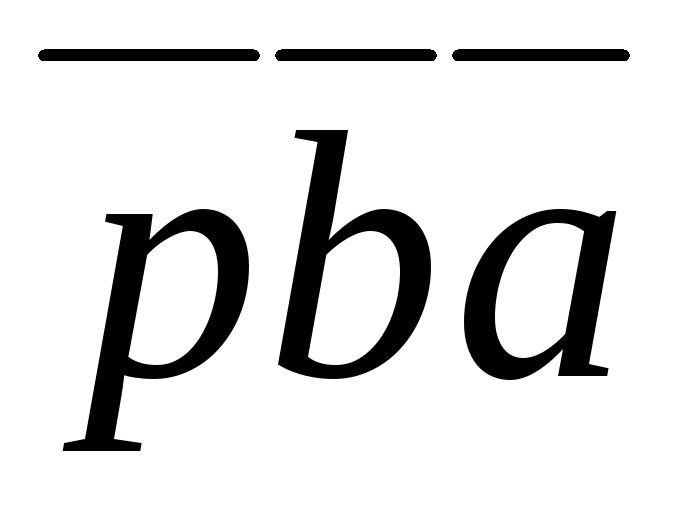)=28−14−18−12+8+7+6−3=2.

Ответ: 2 студента не занимаются ни одним из данных видов спорта.

Решите задачи, предложенные на странице 28, с помощью формулы включений и исключений.

Задача. Сколькими способами можно отправить 8 различных фотографий, использовав при этом 5 различных конвертов?

Решение.Решим задачу, используя формулу включений и исключений.

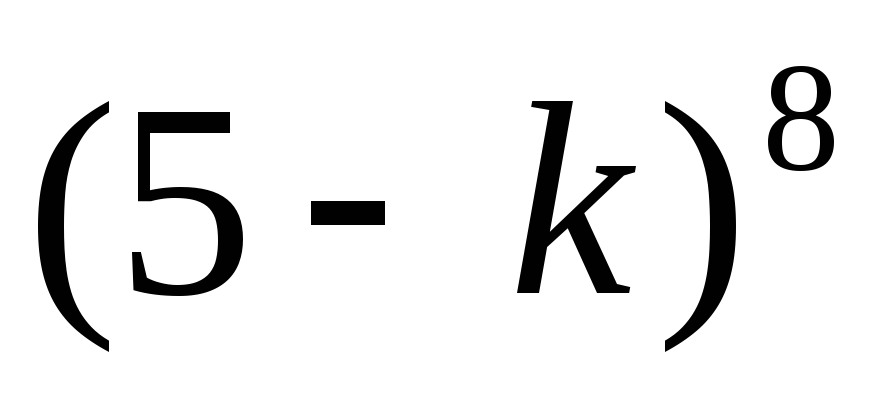
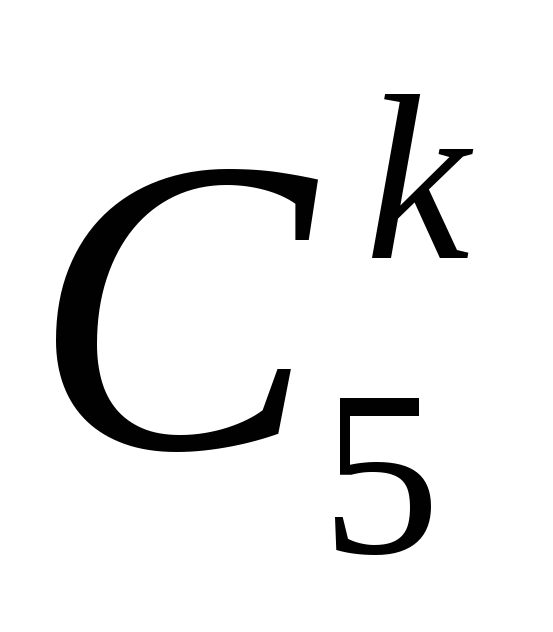
Найдем сначала, при скольких способах распределения данные kконвертов оказываются пустыми (а остальные могут быть как пустыми, так и содержать фотографии). В этом случае фотографии кладутся без ограничений в (5−k) конвертов, число таких распределений равно . Но kконвертов можно выбрать из пяти способами.

Отсюда, применяя формулу включений и исключений, выводим, что число распределений, при которых ни один конверт не оказывается пустым, равно

Ответ: 126000 способами.

Общая задача: сколькими способами можно положить п различных предметов в т различных ящиков так, чтобы в каждом ящике лежал хотя бы один предмет, решается точно такими же рассуждениями.

Число способов распределения выражается формулой:

Рассмотрим общее утверждение.

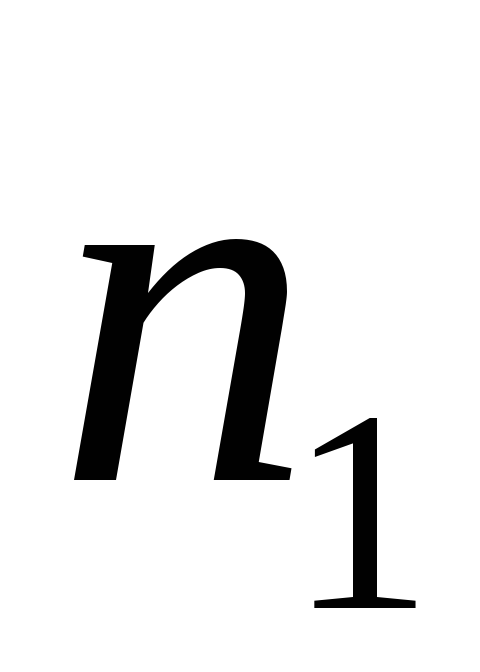
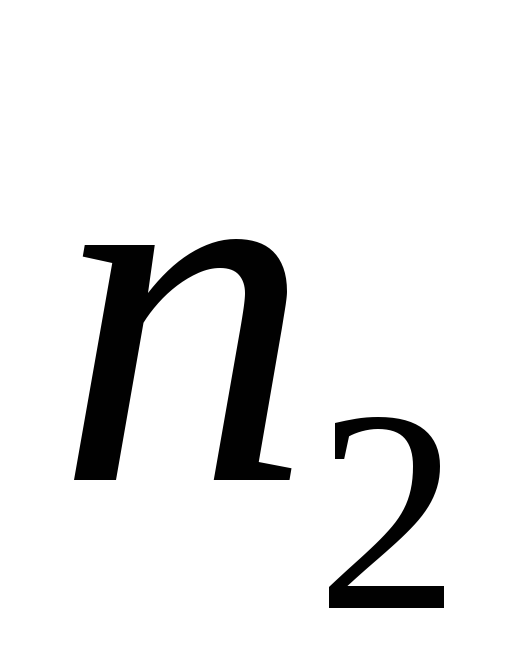
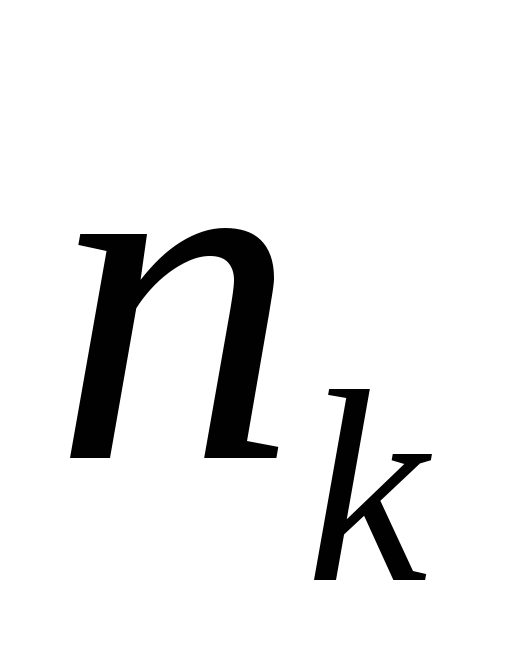
Пусть имеются , предметов первого вида, предметов второго вида, …, предметов k-го вида. Сколькими способами можно раздать их т лицам так, чтобы каждый получил хотя бы один предмет?

Число способов распределения выражается формулой:

Задача. Необходимо разделить 8 яблок, 10 груш и 7 апельсинов между 4 ребятами, при этом каждый должен получить хотя бы один фрукт. Сколькими способами можно это сделать?

Решение.Число способов распределения фруктов между детьми выражается формулой:

Ответ: 5239688 способами.

До сих пор, раскладывая предметы по ящикам, мы не учитывали порядок, в котором могут быть расположены предметы в каждом ящике. Но, например, если речь идет о развешивании сигнальных флагов на мачтах, то имеет значение и порядок вывешиваемых флагов. Решим следующую задачу.

Задача. Имеется n различных сигнальных флагов и mмачт, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке развешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?

Решение.Каждый способ развешивания флагов является комбинацией двух этапов. Первый − определение конфигурации, то есть мест, на которых будут висеть nфлагов на mмачтах. На этом этапе не учитывается ни форма, ни окраска флага, все флаги считаются одинаковыми. Тогда, как мы уже знаем, п флагов можно развесить на mразличных мачтах 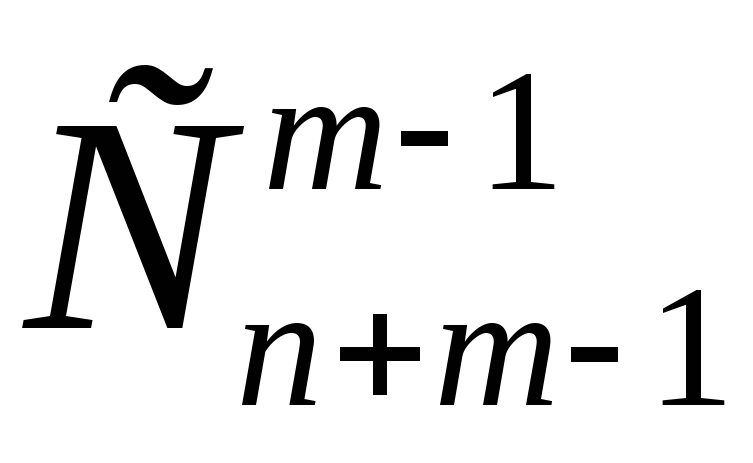способами.

Второй этап − заполнение всех этих nмест конкретными флагами. Это можно сделать n! способами, потому что можно заполнить эти nмест флагами произвольным образом, а потом переставлять флаги друг с другом всевозможными способами, не меняя конфигурации. Число таких перестановок равно n!.

Значит, для каждой конфигурации размещения флагов получается n!конкретных способов развешивания флагов. Общее же число способов развешивания флагов равно:

Вообще, если имеется nразличных предметов, то число способов распределения этих предметов по m различным ящикам с учетом порядка их расположения в ящиках равно

Сколькими способами можно расставить 20 разных книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг?

Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?

Большой класс комбинаторных задач, важных в прикладной математике, сводится к подсчету числа тех или иных расстановок ладей на шахматной доске. Ладья является самой распространенной фигурой в комбинаторных задачах на шахматной доске и часто упоминается даже в серьезной математической литературе.

Задачи о расположении фигур на шахматной доске можно рассматривать как задачи о раскладках. Здесь элементы (фигуры) могут быть различными или одинаковыми, все «ящики» (поля доски) различны, но есть причудливые ограничения в виде связи различных полей.

Цикл комбинаторных задач на шахматной доске связан с подсчетом числа расположений шахматных фигур, при которых они могут бить друг друга или, наоборот, не могут бить друг друга.

Приведем один известный пример из области комбинаторики.

Задача. Пусть требуется назначить n рабочих на n различных работ, причем каждая работа должна выполняться только одним рабочим. Сколькими способами можно осуществить такое назначение?

Решение.Поставим в соответствие рабочим − горизонтали шахматной доски n×n, а работам − ее вертикали. Если i-й рабочий назначается на j-ю работу, то поле, соответствующее пересечению i-й горизонтали и j-й вертикали, займем ладьей. Так как каждая работа выполняется одним рабочим и каждый рабочий назначается на одну работу, то в результате расстановки n ладей все вертикали и горизонтали доски будут содержать по одной ладье, то есть ладьи не могут бить друг друга. Итак, задаче о назначении можно придать шахматную формулировку.

Задача. Сколькими способами можно расставить n ладей, которые не могли бы бить друг друга, на доске размера n×n?

Решение.Заметим, что при любом расположении более n ладей найдется хотя бы одна вертикаль и хотя бы одна горизонталь с двумя или более ладьями, то есть n − это наибольшее число мирных ладей на доске n×n. Одна из расстановок восьми мирных ладей на обычной доске приведена на рисунке 8.

Рис.8

Выясним например, сколько всего существует искомых расстановок n ладей на доске n×n. На первую вертикаль можно произвольно поставить одну из n ладей затем на вторую вертикаль − одну из (n-1) оставшихся ладей, причем горизонталь, занятая первой ладьей исключается (ладьи не должны угрожать друг другу) на третью вертикаль − одну из (n-2) оставшихся (горизонтали, занятые первыми двумя ладьями, исключаются) и т.д., вплоть до (n-1)-й вертикали, на которой для ладьи остается выбор из двух горизонталей, и последней, n-й вертикали, с единственным полем для ладьи. Комбинируя n различных расположений ладьи на первой вертикали с (n-1) расположением на второй, (n-2) − на третьей и т.д., получаем n(n-1)∙…∙2·1=n! различных расположений ладей. Это число и является искомым.

В частности, на обычной доске восемь ладей, не угрожающих друг другу, можно расположить 8!=40320 способами.

Если ладьи занумерованы числами от 1 до n, то существует уже (n!)2 расположений ладей, не угрожающих друг другу. Это следует из того, что n подходящих полей можно выбрать n! способами; столько же способов имеется для расположения на этих полях n занумерованных ладей.

Итак, n рабочих можно назначить на n работ n! различными способами. Пусть выбрано назначение, соответствующее рисунку 7, то есть i-го рабочего назначили на i-ую работу, и требуется сделать новое назначение с учетом того, что каждый рабочий хочет поменять свою предыдущую работу. Сколько существует таких назначений? Эта задача имеет иную ладейную формулировку.

Задача. Сколькими способами можно расставить n не угрожающих друг другу ладей на доске n×n так, чтобы ни одна из них не стояла на главной диагонали?

Решение.Дополнительное условие значительно затрудняет решение задачи. Даже Эйлеру не удалось найти общую формулу для числа указанных расстановок. Позднее была найдена формула, которая имеет следующий вид: .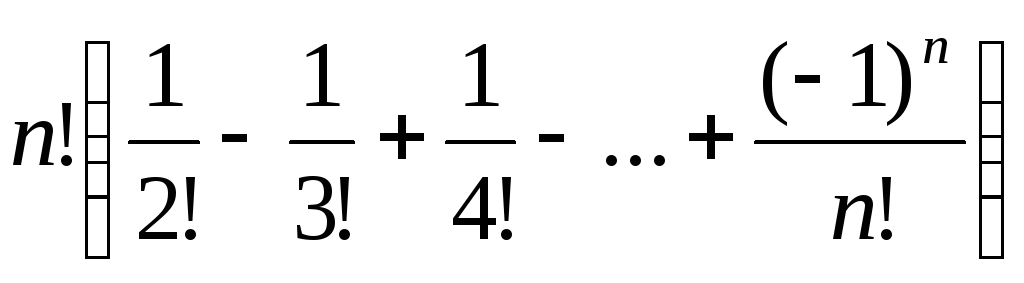

Для n=8 получаем 4833, то есть при дополнительном условии число расстановок восьми ладей, не угрожающих друг другу, уменьшается почти втрое.

Задача. Сколькими способами можно расставить k ладей на m×n доске так, чтобы, они не могли бить друг друга.

Решение.Ясно, что для разрешимости задачи нужно, чтобы выполнялись условия k Источник

Источник

Примеры решения некоторых комбинаторных задач

Задача. Из 28 студентов группы 14 человек занимаются плаванием, 18 человек – баскетболом, 12 студентов – легкой атлетикой, 8 – плаванием и баскетболом, 7 – легкой атлетикой и баскетболом, 6 – плаванием и легкой атлетикой, 3 студентов занимаются и плаванием, и баскетболом, и легкой атлетикой. Сколько в группе студентов, которые не занимаются ни одним из данных видов спорта?

Решение. Обозначим через p − увлечение плаванием, через b − увлечение баскетболом, через a − увлечение легкой атлетикой. Подсчитаем, сколько студентов в данной группе не занимаются ни одним из данных видов спорта, то есть найдем чему равно N().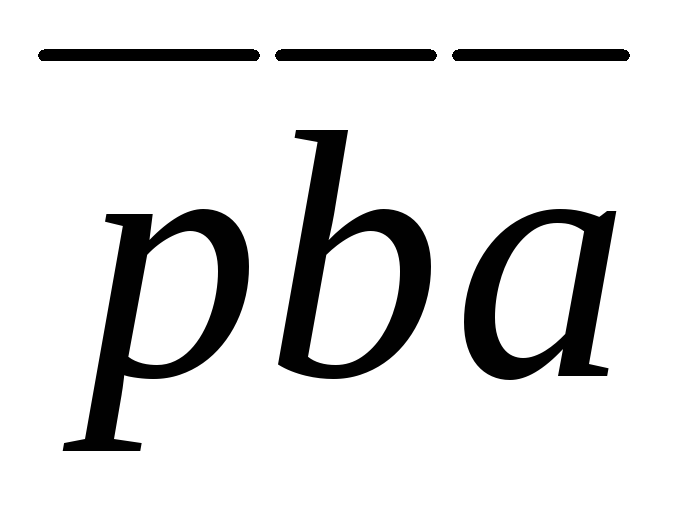

Значит, по формуле включений и исключений получаем, что N(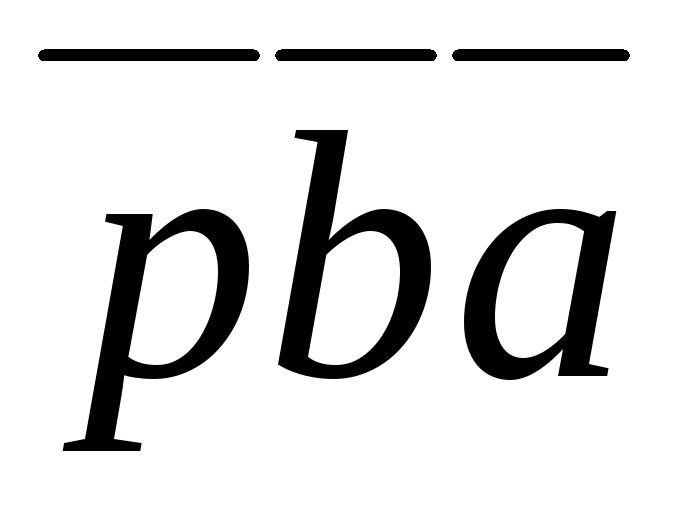)=28−14−18−12+8+7+6−3=2.

Ответ: 2 студента не занимаются ни одним из данных видов спорта.

Решите задачи, предложенные на странице 28, с помощью формулы включений и исключений.

Задача. Сколькими способами можно отправить 8 различных фотографий, использовав при этом 5 различных конвертов?

Решение. Решим задачу, используя формулу включений и исключений.

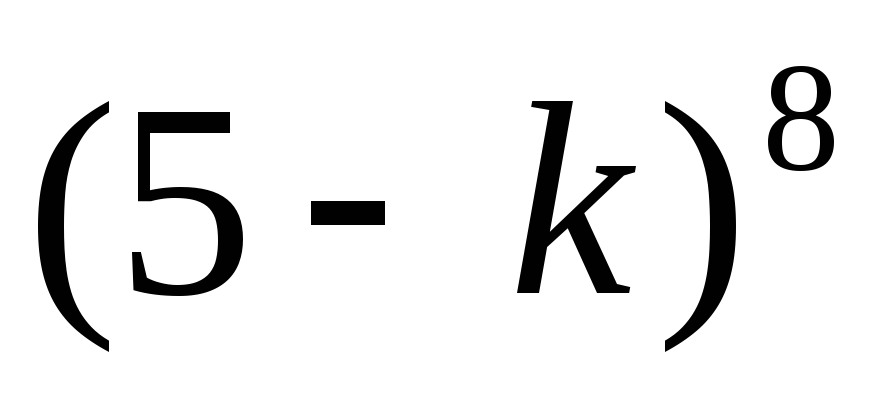
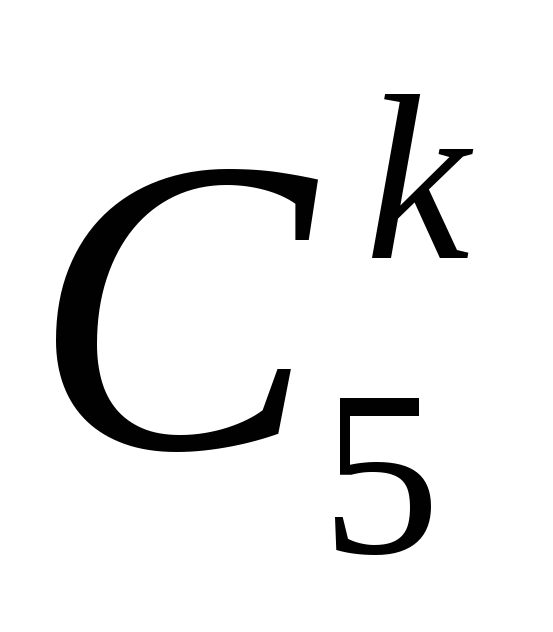
Найдем сначала, при скольких способах распределения данные k конвертов оказываются пустыми (а остальные могут быть как пустыми, так и содержать фотографии). В этом случае фотографии кладутся без ограничений в (5−k) конвертов, число таких распределений равно . Но k конвертов можно выбрать из пяти способами.

Отсюда, применяя формулу включений и исключений, выводим, что число распределений, при которых ни один конверт не оказывается пустым, равно

Ответ: 126000 способами.

Общая задача: сколькими способами можно положить п различных предметов в т различных ящиков так, чтобы в каждом ящике лежал хотя бы один предмет, решается точно такими же рассуждениями.

Число способов распределения выражается формулой:

Рассмотрим общее утверждение.

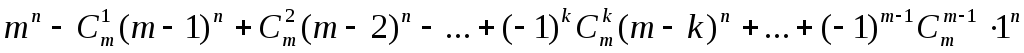
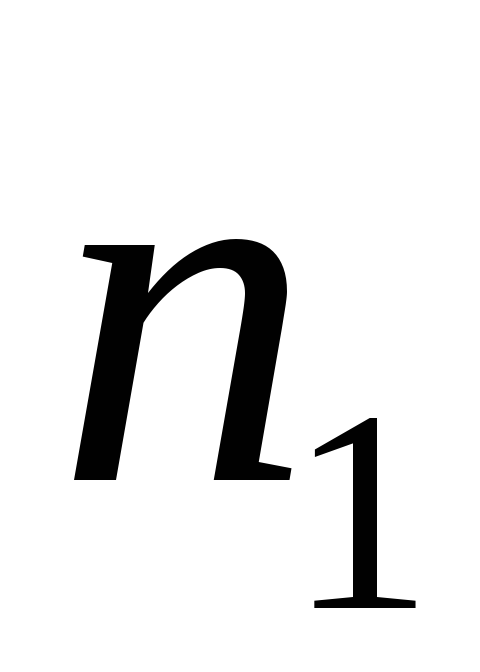
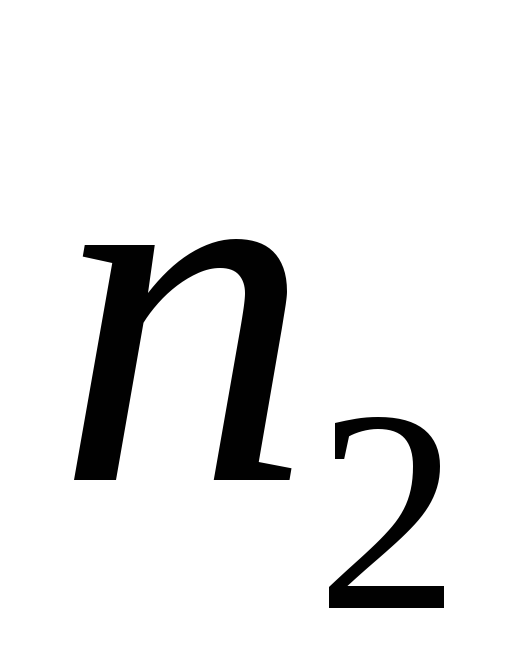
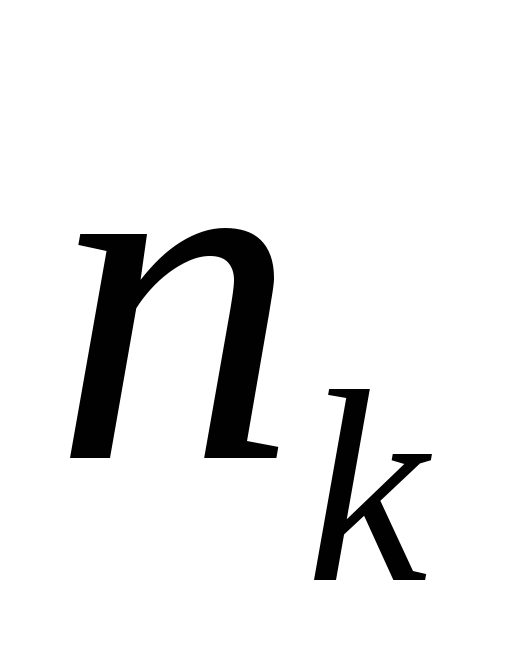
Пусть имеются , предметов первого вида, предметов второго вида, …, предметов k-го вида. Сколькими способами можно раздать их т лицам так, чтобы каждый получил хотя бы один предмет?

Число способов распределения выражается формулой:

Задача. Необходимо разделить 8 яблок, 10 груш и 7 апельсинов между 4 ребятами, при этом каждый должен получить хотя бы один фрукт. Сколькими способами можно это сделать?

Решение. Число способов распределения фруктов между детьми выражается формулой:

Ответ: 5239688 способами.

До сих пор, раскладывая предметы по ящикам, мы не учитывали порядок, в котором могут быть расположены предметы в каждом ящике. Но, например, если речь идет о развешивании сигнальных флагов на мачтах, то имеет значение и порядок вывешиваемых флагов. Решим следующую задачу.

Задача. Имеется n различных сигнальных флагов и m мачт, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке развешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?

Решение. Каждый способ развешивания флагов является комбинацией двух этапов. Первый − определение конфигурации, то есть мест, на которых будут висеть n флагов на m мачтах. На этом этапе не учитывается ни форма, ни окраска флага, все флаги считаются одинаковыми. Тогда, как мы уже знаем, п флагов можно развесить на m различных мачтах 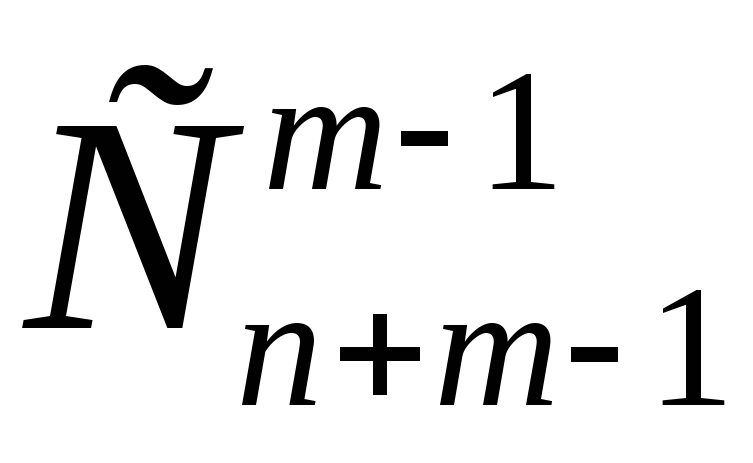способами.

Второй этап − заполнение всех этих n мест конкретными флагами. Это можно сделать n! способами, потому что можно заполнить эти n мест флагами произвольным образом, а потом переставлять флаги друг с другом всевозможными способами, не меняя конфигурации. Число таких перестановок равно n!.

Значит, для каждой конфигурации размещения флагов получается n! конкретных способов развешивания флагов. Общее же число способов развешивания флагов равно:

Вообще, если имеется n различных предметов, то число способов распределения этих предметов по m различным ящикам с учетом порядка их расположения в ящиках равно

Сколькими способами можно расставить 20 разных книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг?

Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?

Большой класс комбинаторных задач, важных в прикладной математике, сводится к подсчету числа тех или иных расстановок ладей на шахматной доске. Ладья является самой распространенной фигурой в комбинаторных задачах на шахматной доске и часто упоминается даже в серьезной математической литературе.

Задачи о расположении фигур на шахматной доске можно рассматривать как задачи о раскладках. Здесь элементы (фигуры) могут быть различными или одинаковыми, все «ящики» (поля доски) различны, но есть причудливые ограничения в виде связи различных полей.

Цикл комбинаторных задач на шахматной доске связан с подсчетом числа расположений шахматных фигур, при которых они могут бить друг друга или, наоборот, не могут бить друг друга.

Приведем один известный пример из области комбинаторики.

Задача. Пусть требуется назначить n рабочих на n различных работ, причем каждая работа должна выполняться только одним рабочим. Сколькими способами можно осуществить такое назначение?

Решение. Поставим в соответствие рабочим − горизонтали шахматной доски n×n, а работам − ее вертикали. Если i-й рабочий назначается на j-ю работу, то поле, соответствующее пересечению i-й горизонтали и j-й вертикали, займем ладьей. Так как каждая работа выполняется одним рабочим и каждый рабочий назначается на одну работу, то в результате расстановки n ладей все вертикали и горизонтали доски будут содержать по одной ладье, то есть ладьи не могут бить друг друга. Итак, задаче о назначении можно придать шахматную формулировку.

Задача. Сколькими способами можно расставить n ладей, которые не могли бы бить друг друга, на доске размера n×n?

Решение. Заметим, что при любом расположении более n ладей найдется хотя бы одна вертикаль и хотя бы одна горизонталь с двумя или более ладьями, то есть n − это наибольшее число мирных ладей на доске n×n. Одна из расстановок восьми мирных ладей на обычной доске приведена на рисунке 8.

Рис.8

Выясним например, сколько всего существует искомых расстановок n ладей на доске n×n. На первую вертикаль можно произвольно поставить одну из n ладей затем на вторую вертикаль − одну из (n-1) оставшихся ладей, причем горизонталь, занятая первой ладьей исключается (ладьи не должны угрожать друг другу) на третью вертикаль − одну из (n-2) оставшихся (горизонтали, занятые первыми двумя ладьями, исключаются) и т.д., вплоть до (n-1)-й вертикали, на которой для ладьи остается выбор из двух горизонталей, и последней, n-й вертикали, с единственным полем для ладьи. Комбинируя n различных расположений ладьи на первой вертикали с (n-1) расположением на второй, (n-2) − на третьей и т.д., получаем n(n-1)∙…∙2·1=n! различных расположений ладей. Это число и является искомым.

В частности, на обычной доске восемь ладей, не угрожающих друг другу, можно расположить 8!=40320 способами.

Если ладьи занумерованы числами от 1 до n, то существует уже (n!) 2 расположений ладей, не угрожающих друг другу. Это следует из того, что n подходящих полей можно выбрать n! способами; столько же способов имеется для расположения на этих полях n занумерованных ладей.

Итак, n рабочих можно назначить на n работ n! различными способами. Пусть выбрано назначение, соответствующее рисунку 7, то есть i-го рабочего назначили на i-ую работу, и требуется сделать новое назначение с учетом того, что каждый рабочий хочет поменять свою предыдущую работу. Сколько существует таких назначений? Эта задача имеет иную ладейную формулировку.

Задача. Сколькими способами можно расставить n не угрожающих друг другу ладей на доске n×n так, чтобы ни одна из них не стояла на главной диагонали?

Решение. Дополнительное условие значительно затрудняет решение задачи. Даже Эйлеру не удалось найти общую формулу для числа указанных расстановок. Позднее была найдена формула, которая имеет следующий вид: .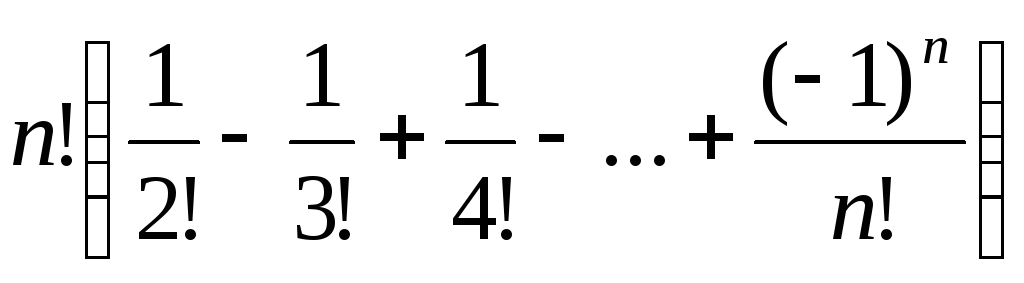

Для n=8 получаем 4833, то есть при дополнительном условии число расстановок восьми ладей, не угрожающих друг другу, уменьшается почти втрое.

Задача. Сколькими способами можно расставить k ладей на m×n доске так, чтобы, они не могли бить друг друга.

Комбинаторные задачи о расстановке атакующих фигур не менее популярны, чем задачи о расстановке мирных фигур. Наиболее просто они решаются для ладьи.

Сколькими способами можно расставить 4 мирных ладьи на доске 8×8, если 2 из них − белые и 2 − черные?

Сколькими способами можно расставить 8 ладей, которые не могли бы бить друг друга, на доске размера 8×8?

Сколькими способами можно расставить 4 ладьи на обычной шахматной доске?

Сколькими способами можно поставить 20 белых шашек на шахматной доске так, чтобы это расположение не менялось при повороте доски на 90°?

Источник