при изучении взаимодействия двух тел их можно рассматривать как замкнутую систему если
Импульс материальной точки. Закон сохранения импульса
Закон сохранения импульса
Пусть система состоит из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.
Запомни
Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не принадлежащим ей, называются внешними силами.
Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола — внешние силы. Пусть на тела некоторой системы действуют внешние силы F1 и F2 (рис. 4.2).

Запомни
Силы, возникающие в результате взаимодействия тел, принадлежащих системе, называются внутренними силами.

Обозначим внутренние силы через 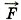
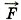
Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за малый промежуток времени At, то для тел системы можно записать второй закон Ньютона в виде
Δ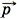
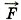
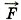
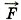
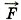
Сложив эти равенства, получим
Δ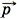
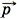
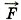
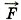
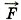
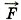
В левой части равенства (4.4) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса самой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы):
Δ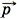
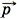
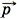
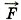
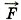
Учитывая равенства (4.4) и (4.6), можно записать:
Δ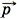
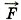
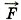
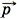
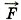
где 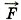
Мы доказали весьма важное положение:
Важно
импульс системы тел могут изменить только внешние силы, причем изменение импульса системы Δрсист совпадает по направлению с суммарной внешней силой.
Внутренние силы изменяют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут.
Уравнение (4.7) справедливо для любого интервала времени Δt, если сумма внешних сил остаётся постоянной.
Из уравнения (4.7) вытекает закон сохранения импульса.
Закон сохранения импульса
Если внешние силы на систему не действуют или их сумма равна нулю, то импульс системы сохраняется:
Δ
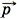
Полученный результат справедлив для системы, содержащей произвольное число тел:
Импульс, очевидно, сохраняется в изолированной системе тел, так как в этой системе на тела вообще не действуют внешние силы. Но область применения закона сохранения импульса шире.
1) Если даже на тела системы действуют внешние силы, но их сумма равна нулю, то импульс системы всё равно сохраняется.
2) Если сумма внешних сил не равна нулю, но сумма проекций сил на какое- то направление равна нулю, то проекция суммарного импульса системы на это направление не меняется.
При изучении взаимодействия двух тел их можно рассматривать как замкнутую систему если
Зная связь ускорения тела со скоростью его движения 
Полученное выражение показывает, что результат действия силы можно понимать и несколько иначе, чем мы делали это раньше: действие силы на тело приводит к изменению некоторой величины, характеризующей это тело, которая равна произведению массы тела на скорость его движения . Эту величину называют импульсом тела 
Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.
Слово «импульс» в переводе с латинского означает «толчок». В некоторых книгах вместо термина «импульс» используется термин «количество движения».
Поскольку 
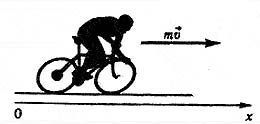
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
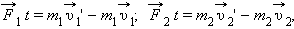 |
где 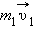
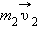
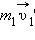
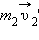
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
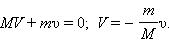 |
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Изменение импульса тела:
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса 
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела
Вопросы.
1. Что называют импульсом тела?
2. Что можно сказать о направлениях векторов импульса и скорости движущегося тела?
Направление вектора скорости v совпадает с направлением вектора скорости v движущегося тела.
3. Что принимают за единицу импульса?
За единицу импульса в СИ принимают импульс тела массой 1 кг, движущегося со скоростью 1 м/с, т.е. 1 кг * м/с (килограмм-метр в секунду).
4. Как ставился опыт, изображенный на рисунке 42, и о чем он свидетельствует?
Описание опыта см. стр. 79-80. Вывод: Этот опыт свидетельствует, что импульс системы из двух шариков остается постоянным.
5. Что означает утверждение о том, что несколько тел образуют замкнутую систему?
Под замкнутой системой понимается такая система на которую не действуют внешние силы. Иными словами тела образуют замкнутую систему, если они взаимодействуют только друг с другом.
6. Сформулируйте закон сохранения импульса.
7. Для замкнутой системы, состоящей из двух тел, запишите закон сохранения импульса в виде уравнения, в которое входили бы масса и скорости этих тел. Поясните, что означает каждый символ в этом уравнении.
1. Две игрушечные заводные машины, массой по 0,2 кг каждая, движутся прямолинейно навстречу друг другу. Скорость каждой машины относительно Земли равна 0,1 м/с. Равны ли векторы импульсов машин? модули векторов импульсов? Определите проекцию импульса каждой из машин на ось Х, параллельную их траектории.
2. На сколько изменится (по модулю) импульс автомобиля массой 1т при изменении его скорости от 54 км/ч до 72 км/ч?
3. Человек сидит в лодке, покоящейся на поверхности озера. В какой-то момент он встаёт и идёт с кормы на нос. Что произойдет при этом с лодкой? Объясните явление на основе закона сохранения импульса.
Так как импульс системы до начала движения человека p =0, то после его движения, по закону сохранения импульса лодка должна начать двигаться в противоположном направлении.
4. Железнодорожный вагон массой 35 т подъезжает к стоящему на том же пути неподвижному вагону массой 28 т и автоматически сцепляется с ним. После сцепки вагоны движутся прямолинейно со скоростью 0,5 м/с. Какова была скорость вагона массой 35 т перед сцепкой?
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1 и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
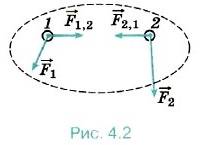
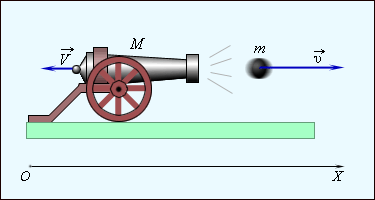
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено




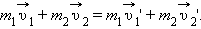







.jpg)
.jpg)
.jpg)
.jpg)
















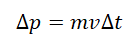






Warning: Use of undefined constant expert_review_likes - assumed 'expert_review_likes' (this will throw an Error in a future version of PHP) in /var/www/www-ars1963/data/www/ck62.ru/wp-content/themes/colormag/comments.php on line 93