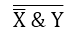какое отношение логика имеет к информатике
Какое отношение логика имеет к информатике
Чеботарева Юлия Владимировна
учитель информатики и ИКТ ГБОУ СОШ №692
Калининского района г.Санкт-Петербурга
Умение думать, логически мыслить, давать ответы на поставленные вопросы всегда играло важную роль в жизни человека. Какую задачу мы обычно называем логической? Это та задача, когда для ее решения требуются определенные логические рассуждения.
Все науки возникли из практики. Те знания, которые лежат в основе разных наук, человек приобретал в борьбе с опасными для него явлениями природы. Человека всегда интересовала истина. Познание истины привело к прогрессу человечества. Главная задача логики состоит в том, чтобы выявить, какие способы рассуждения правильные, а какие нет. Решение задач призвано повысить общую культуру и интуитивные навыки ясного, последовательного и доказательного мышления
Основоположником логики считают Аристотеля, т.к. именно он подверг анализу человеческое мышление, такие его формы, как понятие, суждения, умозаключение, и рассмотрел мышление со стороны строения, структуры, то есть с формальной стороны. Так возникла формальная логика-наука, пытавшаяся найти ответ на вопрос, как мы рассуждаем, изучающая логические операции и правила мышления. В течение многих веков логика помогала математике стать строгой, последовательной наукой. Аристотель систематически изложил логические знания и как гражданин активно участвовал в жизни своего государства. Он регулярно посещал народные собрания, где обсуждались вопросы войны и мира, городского строительства, торговли и т.п., ежегодно участвовал в выборах государственных чиновников и сам в течение жизни неоднократно мог занимать те или иные должности. Античные греки много и с удовольствием судились, причем греческий суд не знал прокуроров и адвокатов, истец и ответчик сами должны были выступать перед судьями и присутствовавшей публикой. От умения внятно изложить суть дела и убедительно обосновать свои претензии часто зависел исход дела. Гражданину необходима была определенная образованность для выполнения своих гражданских обязанностей и осуществления своих гражданских прав.
В Древней Греции приветствовалось получение всеобщего образования и очень высоко ценились учителя, их называли софистами, что означало первоначально «мудрец» или «учитель мудрости». Они учили детей грамоте, основам наук, также воспитывали умение говорить красиво и убедительно, уметь отстаивать в спорах свое мнение. Вскоре софисты стали изобретать приемы, для того, чтобы, чтобы одурачить собеседника и представить противника в смешном или глупом виде, внушить недоверие к истине, а ложь, напротив, представить как истину. Такие лживые приемы получили название «софизмы», а слово «софист» приобрело негативный оттенок, который сохранился у него до сих пор. Вот примеры некоторых софизмов, сохранившихся в трудах древних авторов: «Сидящий встал. Кто встал, тот стоит. Следовательно, сидящий стоит».
«Со времен Античности до нас дошла следующая история. У знаменитого софиста Протагора был ученик по имени Эватл, обучавшийся праву. Учитель и ученик заключили договор, согласно которому Эватл должен был заплатить за обучение лишь после того, как выиграет свой первый процесс. Однако, закончив обучение, Эватл не спешил выступать в суде. Терпение учителя иссякло, и он подал на своего ученика в суд.«Эватл в любом случае вынужден будет заплатить мне, – рассуждал Протагор. – Он либо выиграет этот процесс, либо проиграет его. Если выиграет – заплатит в силу нашего с ним договора; если же проиграет – заплатит в силу приговора суда». «Ничего подобного, – рассуждал, в свою очередь, Эватл. – Действительно, я либо выиграю процесс, либо проиграю его. Если выиграю – решение суда освободит меня от уплаты; если же проиграю – не буду платить в силу нашего договора». Ученик оказался достоин своего учителя!»
Аристотель систематизировал известные к тому времени логические знания, добавив к ним немало нового, и написал несколько сочинений, в которых представил логику как средство защиты истины и разоблачения софистики и лжи. В этом качестве она служит людям вот уже более двух тысячелетий.
В середине XIX в. логика пережила свою научную революцию: возникла и стала бурно развиваться математическая логика, применяющая для анализа рассуждений математические средства и методы. Она заложила теоретические основы последующей разработки языков программирования для компьютерной техники. Аристотелевская логика с тех пор стала называться традиционной.
Области применения логики в компьютерных науках расширяются с каждым годом. Чтобы быть хорошим программистом нужно не только знать теорию, необходимо также логически и правильно мыслить. Без логики программирование не существовало бы. Основы логики одни, но в разных областях, логика применяется по-разному. Логика в информатике играет особую роль, так как она позволяет доказать правильность определенных программ и алгоритмов. Любая программа проходит тестирование на правильность, но доказать правильность можно только путем логического мыслительного процесса.
Растущее значение компьютерной грамотности говорит о важности знания логики, которая является одной из теоретических основ электронно-вычислительной техники. Изучение логики развивает ясность и четкость мышления. Логика обладает способностью уточнять предмет мысли. Она развивает внимательность, аккуратность, убедительность в суждениях, а также умение абстрагироваться от конкретного содержания и сосредоточиться на структуре своей мысли.
Логика и компьютер
Вы будете перенаправлены на Автор24
Логика в информатике – это те отрасли знания и направления исследований, в которых логика применяется в информатике и искусственном интеллекте. В информатике логика оказалась гораздо более эффективной, чем это было в математике.
Основные направления прикладного использования логики в информатике
Стандартное математическое представление любого вычисления − это отображение переменных (их внутреннего состояния) вычислительного устройства на входе в новое состояние на выходе. В алгебре логики решается стандартная задача, а именно: определяется функциональная полнота логических связок, то есть проверяется, является ли фиксированный набор логических операций достаточным для того, чтобы представить новое результирующее значение путём комбинации любых других (базовых) функций. А это значит, что базовые логические устройства должны быть универсальными и позволять решать большое число задач.
Работу большинства вычислительных устройств, которые существуют в настоящее время, прекрасно описывает алгебра логики, разработанная Джорджем Булем. К таким устройствам относятся триггеры, сумматоры, группы переключателей, Кроме того булева алгебра и компьютеры связаны между собой при помощи используемой в ЭВМ двоичной системы счисления. Поэтому в устройствах компьютера можно хранить и преобразовывать и значения логических переменных, и числа.
Логические элементы — это электронные устройства, которые по определенному закону преобразуют проходящие через них двоичные электрические сигналы.
Готовые работы на аналогичную тему
Все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.
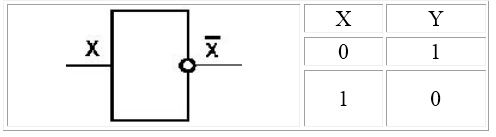
Логический элемент НЕ (инвертор). Простейший логический элемент, реализующий функцию отрицания (инверсию). Унарный элемент – элемент, у которого один вход и один выход.
На функциональных схемах обозначается
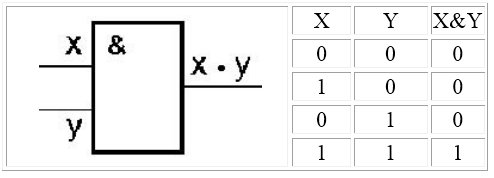
Логический элемент И (конъюнктор) реализует умножение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:
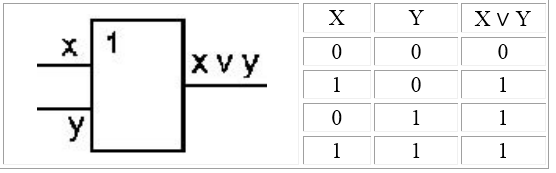
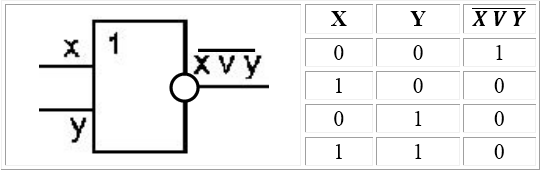
Логический элемент ИЛИ (дизъюнктор) реализует сложение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:
Роль базовых логических элементов в создании схем играют ещё два логических элемента: И-НЕ и ИЛИ-НЕ.
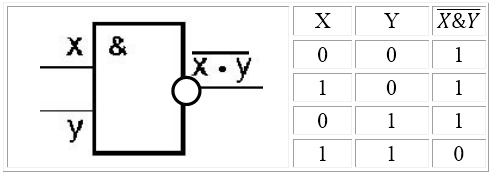
Логический элемент И-НЕ (отрицание конъюнкции) выполняет логическую функцию штрих Шеффера. Операция бинарная, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается следующим образом:
Логический элемент ИЛИ-НЕ (отрицание дизъюнкции) выполняет логическую функцию стрелка Пирса. Тоже бинарная операция, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается так:
Функциональные схемы
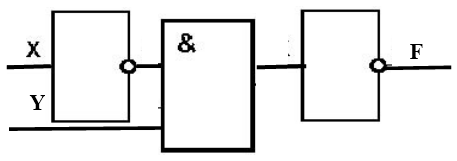
Сигнал, который вырабатывает один логический элемент, можно подать на вход другого элемента. Это даст возможность образовать цепочку из отдельных логических элементов – функциональную схему.
Функциональная (логическая) схема – это схема, которая выполняет определённую функцию и состоит из базовых логических элементов. Проанализировав фунциональную схему, можно понять, как работает логическое устройство, то есть ответить на вопрос, какую же функцию она выполняет. А чтобы описать функциональную схему, нужна структурная формула.
Как по заданной функциональной схеме записать структурную формулу?
Записали, что структурной формулой данной функциональной схемы является формула
Для функциональной схемы нужно составить таблицу значений сигналов на входах и выходах схемы, по которой можно понять, какую функцию выполняет данная схема, – таблицу истинности.
Обработка любой информации на компьютере − выполнение процессором различных арифметических и логических операций. Для этого в составе процессора есть арифметико-логическое устройство (АЛУ), которое состоит из ряда устройств, построенных на логических элементах, рассмотренных выше. Главными устройствами являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.
Конструируется логическое устройство по следующему алгоритму:
Тема «Логика» в курсе информатики
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Логика в курсе информатики Бражникова М.Р. учитель МОУ гимназии имени А.Л. Кекина г.Ростова Январь 2016 год
Преимущества изучения ЛОГИКИ в курсе информатики Знакомство с терминологией и символикой алгебры логики, с ее понятиями помогает развитию мыслительных способностей, развивает логическое мышление. При решении логических задач учащиеся достаточно легко привыкают к требованию формализации условий задачи и построению модели решения задачи. Знание логических операций и умение строить сложные логические выражения помогают ребятам быстрее изучить условные выражения и условные операторы языка программирования и меньше ошибаться при их использовании. Самостоятельно построив логическую схему хотя бы одного простого устройства, учащиеся лучше представляют себе архитектуру и принцип функционирования компьютера. Алгебра логики- это мощный инструмент пользователя в базах данных и информационно-поисковых системах.
Подходы к рассмотрению темы в современных авторских программах основной школы Авторский коллектив Семакина: Основы математической логики не изучаются в качестве отдельной темы, а вводятся по мере необходимости при работе с конкретным практическим модулем (например, Базы данных). Логические основы ЭВМ не рассматриваются вообще. Авторские коллективы Угриновича, Макаровой и Босовой: Учащиеся знакомятся с элементами формальной логики в виде самостоятельной темы, а уже закрепление и использование полученных знаний происходит при работе с модулями: «Моделирование и формализация», «Базы данных» (Н.Д. Угриновича); «Освоение среды табличного процессора Excel» (авт. коллектив Н.В. Макаровой); «Математические основы информатики» (Л.Л. Босова)
Основная школа I. Введение в логику. Знакомство с формальной логикой История становления логики как науки. Формы человеческого мышления и их характеристики. Круги Эйлера для отображения объёмов понятий и отношений между ними. Основной принцип формальной логики. II. Знакомство с алгеброй высказываний Понятие об алгебре высказываний. Логические операции. Построение таблиц истинности сложных высказываний. Тождественно истинные и тождественно ложные высказывания. Логические функции. Построение таблиц истинности с помощью электронных таблиц.
Методические особенности организации уроков В качестве основных методов проверки теоретических знаний используется устный опрос диктант тестирование письменная работа. Большая роль отводится самоконтролю. Для закрепления навыков работы с программными средствами используется лабораторная работа. Итоговый контроль по теме проводится в виде контрольной работы или зачёта.
Фрагмент урока «Связь между алгеброй логики и теорией множеств» (профиль) В курсе основной школы вы уже встречались с кругами Эйлера и знаете какие между множествами могут быть отношения. Для графической иллюстрации логических операций можно также воспользоваться диаграммами Эйлера-Венна. Как вы думаете какие операции в теории множеств соответствуют инверсии, конъюнкции и дизъюнкции? Приведите конкретные примеры. Сами рисуют. Инверсия Конъюнкция Дизъюнкция Дополнение к множеству Пересечение множеств Объединение множеств Как бы вы с помощью диаграмм Эйлера-Венна отобразили бы логические операции импликации и эквивалентности? Задание не простое и конечно можно воспользоваться таблицами истинности для данных операций. Ответы учеников: для импликации заштрихуем на диаграмме три области, в которых значения А В равно 1; для эквивалентности две области, для которых значения А В равны 1. Импликация Эквивалентность Учитель подводит итог: для импликации в теории множеств соответствующей операции нет, тем не менее можно отобразить импликацию с помощью диаграммы Эйлера-Венна; логической операции эквивалентности в теории множеств соответствует операция эквивалентности множеств.
Какое отношение логика имеет к информатике
Логика – это бог мыслящих…
Не мыслям надобно учить, а мыслить.
Два основных достояния человеческой природы
это ум и рассуждения.
Мы истинно свободны, когда имеем
способность рассуждать самостоятельно.
В нашей повседневной жизни случается так, что нам недостает сведений о каком-то интересующем нас предмете. Тогда мы обращаемся за помощью к учебникам, справочникам, энциклопедиям или же спрашиваем у специалистов.
Первое упоминание логики встречается в китайской «Книге перемен»(VIII в. до н.э.). В Древней Греции она начала разрабатываться в VI в. до н.э. Немного позже логика возникла в Индии. Первоначально логика служила юриспруденции и ораторскому искусству. Еще одним стимулом создания науки логики стали запросы математики, где требовались строгие доказательства.
Первые общие схемы правильных рассуждений систематически были изложены уже в древности греческим философом Аристотелем (384-322 г. до н. э.). Независимо от него несколько иными видами схем правильных умозаключений и другие философы. Затем в средние века были несколько развиты и пополнены древние схемы умозаключений. Позже, в новое время, некоторый прогресс в логике наступил благодаря философу и математику Г. В. Лейбницу (1646-1716). Великий русский и швейцарский ученый Леонард Эйлер(1707-1783) с 1727г. по 1741г. работал в России. С 1766г. был избран академиком Петербургской АН. Ученый необычайной широты интересов. Автор свыше 800 работ по математике, физике, небесной механике, оптике, баллистике, кораблестроению, теории музыки. Предложил так называемые круги Эйлера, ставшие основой формальной логики.
Основоположником математической логики считается Джордж Буль(1815-1864),английский математик, отец всемирно известной писательницы Этель Лилиан Войнич.
Со второй половины XIX и в ХХ вв. благодаря работам Дж. Буля, Г. Фреге (1848-1925) и других ученых в логике начался период интенсивного развития, приведшего к тому, что логика стала самостоятельной, содержательной научной дисциплиной. Этот последний период бурного развития логики имеет своим источником разработку вопросов обоснования математики. В самом деле, математика представляет собой такую науку, в которой умозаключение играет более важную роль по сравнению с другими науками. Все математические теоремы опираются на точные доказательства, основанные на выводе следствий из общепринятых общих математических аксиом или постулатов. Поэтому неудивительно, что ученые при анализе математических рассуждений открыли в этих рассуждениях больше всего схем (способов) правильного умозаключения.
В дальнейшем мы будем рассматривать так называемую логику высказываний. На ее примере мы ближе познакомимся с тем, на чем основаны современные логические схемы правильных умозаключений и каким образом в современной логике мы пользуемся логическими символами. Тем самым мы познакомимся с основными понятиями формальной и математической логики.
Формальная логика помогает справиться с обработкой большого объема информации при анализе и синтезе, при решении разнообразных задач, при составлении алгоритмов и программ. В настоящее время значение логики сильно возросло в связи с насущной необходимостью создания искусственного интеллекта.
Среди ранних приобретений детского разума огромную ценность представляет язык, его словарный фонд и грамматика. Не меньшую ценность имеет умение логически правильно мыслить. Незаметно и быстро оно усваивается в детстве.
Логическая наука сегодня – это сложное, системное знание, включающее в себя множество отраслей: логическая семиотика, символическая логика, диалектическая логика и др.
Логику, в первую очередь, интересует не то, как мыслит человек, а то, как он должен мыслить для решения задач познавательного характера, для достижения истины. Таким образом, логикой являются исторически сложившиеся формы и приемы познания, от которых зависит истинность результата познания.
Логика в информатике
Содержание
Область применения
Включаются следующие основные применения:
Этот список продолжает пополняться.
Эффективность логики в компьютерных науках
В отличие от естественных наук, компьютерные науки получили большой стимул от широкого и непрерывного взаимодействия с логикой. Особую роль в компьютерных науках играют доказательные методы разработки алгоритмов и программ с доказательствами их правильности.
Тестирование программ может выявить наличие ошибок в программах, но не может гарантировать их отсутствие. Гарантии отсутствия ошибок в алгоритмах и программах могут дать только доказательства их правильности. Алгоритм не содержит ошибок, если он дает правильные решения для всех допустимых данных.
Серьёзнейшей проблемой для компьютерных наук и информатики является наличие ошибок в алгоритмах и программах, публикуемых в учебниках и учебных пособиях, а также неумение преподавателей и учителей информатики выявлять и исправлять ошибки в алгоритмах и программах, составленных учащимися.
Единственный путь для преодоления этих проблем—это изучение систематических методов составления алгоритмов и программ с одновременным анализом их правильности в рамках доказательного программирования с самого начала обучения основам алгоритмизации и программирования.
Сложность для преподавателей и программистов заключается в том, что они должны уметь писать не только алгоритмы и программы, но и доказательства правильности своих алгоритмов и программ. Что сейчас не умеют делать ни математики, ни программисты.
В результате программисты пишут программы с большим числом ошибок, которые они не могут ни выявить, ни исправить. Массированное тестирование программ на ЭВМ приносит программистам несомненную пользу, однако не дает гарантий полного избавления от ошибок.
Практика применения и изучения доказательных методов программирования показала, что эта технология вполне доступна студентам математических факультетов, которым вполне по силам написание доказательств правильности алгоритмов, после проверки и тестирования программ на ЭВМ.
Наибольший эффект в освоении технологий доказательного программирования наблюдается в олимпиадах по информатике и программированию, где победителями и призёрами становятся те студенты, которые освоили технику тестирования программ на ЭВМ и составления алгоритмов и программ без ошибок.