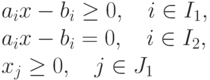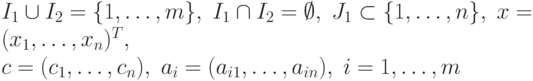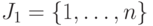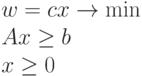какое ограничение называется активным в задачах линейного и нелинейного программирования
Прикладное применение задачи нелинейного программирования
Доброго времени суток, Хабр! В свое время, будучи студентом младших курсов, я начал заниматься научно-исследовательской работой в области теории оптимизации и синтеза оптимальных нелинейных динамических систем. Примерно в то же время появилось желание популяризировать данную область, делиться своими наработками и мыслями с людьми. Подтверждением этому служит пара-тройка моих детских незрелых статей на Хабре. Тем не менее, на тот момент эта идея оказалась для меня непосильной. Возможно ввиду моей занятости, неопытности, неумения работать с критикой и советами или чего-то еще. Можно до бесконечности пытаться найти причину, но ситуацию это не изменит: я забросил эту идею на полку, где она благополучно лежала и пылилась до этого момента.
Закончив специалитет и готовясь к защите кандидатской диссертации, я задался вполне логичным вопросом: «а что же дальше?» Имея за плечами опыт как обычной работы, так и исследовательской, я вновь вернулся к той самой идее, которая, казалось бы, должна была утонуть под толщей пыли. Но вернулся я к этой идее в более осознанной форме.
Я решил заняться разработкой программного обеспечения, связанного с той отраслью, которой занимаюсь уже на протяжении 8 лет, и моими личными академическими пристрастиями, которые включают в себя методы оптимизации и машинное обучение.
Ну что ж, всем заинтересовавшимся:
Занимаясь реализацией программного обеспечения для своего диплома (и впоследствии диссертации), я подходил к этому вопросу «в лоб»: меня не волновало, насколько создаваемая система будет гибкой, как легко она будет модифицируема. Желание получить результат здесь и сейчас вкупе с неопытностью приводили к тому, что код постоянно приходилось переписывать, что, конечно же, не влияло положительно на профессиональное развитие. Уже сейчас я понимаю, что, как бы ни хотелось, нельзя сломя голову бросаться решать задачу. Надо вникнуть в ее суть, оценить имеющиеся знания, понять, чего недостает, сопоставить понятия предметной области классам, интерфейсам и абстракциям. Словом, нужно осознать имеющиеся резервы и грамотно подойти к проектированию архитектуры программного приложения.
Как вы уже догадались, эта статья будет посвящена разработке и описанию первых элементов будущего приложения.
Определение подхода к разработке и формулировка основной задачи
На Хабре есть большое количество статей, посвященных методологиям разработки ПО. Например, в этой достаточно понятно описаны основные подходы. Остановимся подробнее на каждом из них:
Итак, на данный момент имеется следующая формулировка общей задачи: разрабатываемое программное обеспечение, должно реализовывать различные алгоритмы оптимизации (как и классические аналитические, так и современные эвристические) и машинного обучения (алгоритмы классификации, кластеризации, редукции размерности пространства, регрессии). Итоговой финальной целью является разработка методик применения данных алгоритмов в области синтеза оптимального управления и создания торговых стратегий на финансовых рынках. В качестве основного языка для разработки был выбран Scala.
Итак, в этой работе я расскажу:
Оптимизация
Вследствие того что большую часть своей исследовательской практики я посвятил решениям задачи оптимизации, мне будет удобней оперировать именно с этой точки зрения.
Обычно под решением задачи оптимизации, как бы это банально и косноязычно ни звучало, понимается поиск некоторого «оптимального» (с точки зрения условий задачи) объекта. Понятия «оптимальности» варьируются от одной предметной области к другой. Например, в задаче поиска минимума функции требуется найти точку, которой соответствует наименьшее значение целевой функции, в задача мета-оптимизации требуется определить параметры алгоритма, при которых он дает наиболее точный результат/наиболее быстро отрабатывает/дает наиболее стабильный результат, в задаче синтеза оптимального управления требуется синтезировать контроллер, позволяющий перевести объект в терминальное состояние за наименьшее время и т.д. Уверен, что каждый специалист сможет продолжить это список задачами, связанными с его профессиональной сферой.
В математике, особое внимание уделяется задаче нелинейного программирования, к которой можно свести большое количество других прикладных задач. В общем случае, для постановки задачи нелинейного программирования требуется задать:
Существует огромное количество алгоритмов решения этой задачи. Условно их можно разделить на две группы:
Используемые абстракции
На основе приведенных ранее рассуждений мне кажется, что проще всего работать с двумя понятиями: преобразование и алгоритм. На них и остановимся подробнее.
Преобразования (Transformations)
Вследствие того что почти любую процедуру/функцию/алгоритм можно рассматривать как некоторое преобразование, будем оперировать с этим объектом как с одним из базовых.
Предлагается следующая иерархия между различными типами преобразований:
Остановимся на элементах поподробнее:
Приведенные абстракции, на первый взгляд, охватывают основные типы преобразований, который могут понадобится для дальнейших формулировок задач.
Алгоритм
Я думаю, что естественным будет определить алгоритм как набор трех операций: инициализация, итеративная часть и терминация. На вход алгоритма подается некоторое задание (Task). В ходе инициализации происходит генерация начального состояния (State) алгоритма, которое модифицируется в ходе повторения итеративной части. В конце с помощью процедуры терминации из последнего состояния алгоритма создается объект, соответствующий типу R выходного параметра алгоритма.
Таким образом, для создания конкретного алгоритма, необходимо будет переопределить три описанные ранее процедуры.
K-Means VS. Random Search
Что ж, первые два пункта обещанной программы освещены, пора переходить к третьему.
Оба алгоритма хорошо описаны в различных источниках, поэтому я думаю, что у читателей не составит труда разобраться с ними. Вместо этого я проведу параллели к описанным ранее абстракциям.
Кластеризатор, построенный с помощью алгоритма K-Means однозначно определяется своими центроидами. Сам алгоритм K-Means представляет собой постоянную замену текущих центроид новыми центроидами, рассчитанными как среднее значение всех векторов в отдельно взятых кластерах. Таким образом, в любой момент времени состояние алгоритма K-Means можно представить как набор векторов.
Таким образом, кластеризатор может быть построен либо напрямую с помощью алгоритма K-Means, либо с помощью решения задачи поиска оптимального кластеризатора, обеспечивающего минимум суммарного расстояния точек кластеров от соответствующих центроид.
Сгенерируем несколько синтетических наборов данных размерности 2, 3 и 5.
Лекция 3: Математическое программирование. Линейное программирование. Виды задач линейного программирования. Постановка задач линейного программирования и исследование их структуры. Решение задач линейного программирования симплекс-методом
1. Понятие математического программирования
Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.
Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.
Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.
Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач.
В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:
2. Понятие линейного программирования. Виды задач линейного программирования
Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности.
Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира.
Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д.
Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Общая форма задачи имеет вид: найти 
Наряду с общей формой широко используются также каноническая и стандартная формы. Как в канонической, так и в стандартной форме
Задача ЛП в канонической форме:
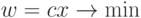 | ( 2.1) |
 | ( 2.2) |
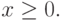 | ( 2.3) |
Задача ЛП в стандартной форме:
Задача ЛП в общей форме сводится (в определенном смысле) к задаче ЛП в канонической (стандартной) форме. Под этим понимается существование общего способа построения по исходной задаче (в общей форме) новой задачи ЛП (в нужной нам форме), любое оптимальное решение которой «легко» преобразуется в оптимальное решение исходной задачи и наоборот. (Фактически, связь между этими задачами оказывается еще более тесной). Тем самым мы получаем возможность, не теряя общности, заниматься изучением задач ЛП, представленных либо в канонической, либо в стандартной форме. Ввиду этого наши дальнейшие рассмотрения задач ЛП будут посвящены, главным образом, задачам в канонической форме.
Математическое программирование. Линейное и нелинейное программирование
Характеристика математического программирования как отдельной дисциплины. Понятие линейного, нелинейного и динамического программирования. Методы решения задач: графический, симплексный методы; постановка двойственной задачи; метод множителей Лагранжа.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 15.08.2014 |
| Размер файла | 71,5 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Размещено на http://www.allbest.ru/
Линейное и нелинейное программирование
1. Понятие математического программирования
2. Понятие линейного программирования. Виды задач линейного программирования
3. Понятие нелинейного программирования
4. Динамическое программирование
Пример (задача линейного программирования)
Известно, что определенный вид продукции можно произвести, используя различные технологические способы; в некоторых производствах возможна взаимозаменяемость материалов; один и тот же тип оборудования может быть использован для производства различных видов продукции и т.п.
Как лучше организовать производство, по каким ценам выгодно производить продукцию, как лучше всего использовать производственные ресурсы, которые высвобождаются и т.п.?
На все эти вопросы позволяет получить ответ математическое программирование, являющееся действенным инструментом принятия решений.
Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.
В зависимости от свойств функций f и gi математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.
Прежде всего задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции f и gi линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования. Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач линейного программирования разработан целый ряд эффективных методов, алгоритмов и программ. Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.
математический программирование динамический лагранж
1. Понятие математического программирования
Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.
Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.
Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач.
В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:
· задачи линейного программирования,
· задачи нелинейного программирования;
· задачи динамического программирования.
2. Понятие линейного программирования. Виды задач линейного программирования
Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности.
Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира.
Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д.
Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Существует несколько методов решения задач ЛП:
Ш Графический метод решения задачи ЛП;
Ш Симплексный метод;
Ш Решение задачи ЛП средствами табличного процессора Excel;
3. Понятие нелинейного программирования
В большинстве инженерных задач построение математической модели не удается свести к задаче линейного программирования.
В данной работе будет рассматриваться такой метод решения задач НП, как метод множителей Лагранжа.
Метод множителей Лагранжа позволяет отыскивать максимум (или минимум) функции при ограничениях-равенствах. Основная идея метода состоит в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой построенной функции Лагранжа.
4. Динамическое программирование
Динамическое программирование представляет собой математические аппарат, позволяющий быстро находить оптимальное решение в случаях, когда анализируемая ситуация не содержит факторов неопределенности, но имеется большое количество вариантов поведения, приносящих различные результаты, среди которых необходимо выбрать наилучший. Динамическое программирование подходит к решению некоторого класса задач путем разложения на части, небольшие и менее сложные задачи. В принципе, задачи такого рода могут быть решены путем перебора всех возможных вариантов и выбора среди них наилучшего, однако часто такой перебор весьма затруднен. В этих случаях процесс принятия оптимального решения может быть разбит на шаги (этапы) и исследован с помощью метода динамического программирования.
Решение задач методами динамического программирования проводится на основе сформулированного Р.Э.Беллманом принципа оптимальности: оптимальное поведение обладает тем свойством, что каким бы ни было первоначальное состояние системы и первоначальное решение, последующее решение должно определять оптимальное поведение относительно состояния, полученного в результате первоначального решения.
Таким образом, планирование каждого шага должно проводится с учетом общей выгоды, получаемой по завершении всего процесса, что и позволяет оптимизировать конечный результат по выбранному критерию.
Вместе с тем динамическое программирование не является универсальным методом решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и требует проведения поиска наиболее приемлемой совокупности методов для ее решения. Кроме того, большие объемы и трудоемкость решения многошаговых задач, имеющих множество состояний, приводят к необходимости отбора задач малой размерности либо использования сжатой информации.
Динамическое программирование применяется для решения таких задач, как: распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом и запасами; составление календарных планов текущего и капитального ремонтов оборудования и его замены; поиск кратчайших расстояний на транспортной сети и т.д.
Все решения задачи разбиваются на два этапа. На первом этапе, который называют условной оптимизацией, отыскиваются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего.
После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый, производится второй этап решения задачи, который называется безусловной оптимизацией.
В общем виде задача динамического программирования формулируется следующим образом: требуется определить такое управление X*, переводящее систему из начального состояния S0 в конечное состояние Sn, при котором целевая функция F(S0,X*) принимает наибольшее (наименьшее) значение.
Особенности математической модели динамического программирования заключаются в следующем:
задача оптимизации формулируется как конечный многошаговый процесс управления;
целевая функция является аддитивной и равна сумме целевых функций каждого шага
выбор управления Xk на каждом шаге зависит только от состояния системы к этому шагу Sk-1 и не влияет на предшествующие шаги (нет обратной связи);
состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk-1 и этого управляющего воздействия Xk (отсутствие последействия) и может быть записано в виде уравнения состояния:
на каждом шаге управление Xk зависит от конечного числа управляющих переменных, а состояние системы Sk зависит от конечного числа переменных;
оптимальное управление X* представляет собой вектор, определяемый последовательностью оптимальных пошаговых управлений:
число которых и определяет количество шагов задачи.
Условная оптимизация. Как уже отмечалось выше, на данном этапе отыскиваются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего в соответствии с алгоритмом обратной прогонки. На последнем n-м шаге найти оптимальное управление X*n и значение функции Беллмана Fn(S) не сложно, так как
где максимум ищется по всем возможным значениям Xn.
Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге:
Этот максимум (или минимум) определяется по всем возможным для k и S значениям переменной управления X.
Безусловная оптимизация. После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый (на первом шаге k=1 состояние системы равно ее начальному состоянию S0), осуществляется второй этап решения задачи. Находится оптимальное управление на первом шаге X1, применение которого приведет систему в состояние S1(S,x1*), зная которое можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге, и так далее до последнего n-го шага.
Для заданной математической постановки задачи ЛП, приняв дополнительно условие неотрицательности переменных, выполнить следующие действия:
Решить задачу графическим методом;
Привести задачу к канонической форме записи;
Составить симплексную таблицу;
Произвести решение задачи симплексным методом ручным способом или с использование компьютера;
Осуществить постановку двойственной задачи ЛП;
Получить решение двойственной задачи из полученной ранее симплексной таблицы и произвести анализ полученных результатов;
Проверить результаты решения в табличном процессоре Excel;
Составить отчет с приведение результатов по каждому пункту.
Какое ограничение называется активным в задачах линейного и нелинейного программирования
Ибо самое странное, заставляющее быть настороже в этой среде, или мире, в котором мы вынуждены существовать, состоит в том, что в пределах неумолимо очерченного всегда представляет нам разнообразные возможности действия, и нам не остается ничего, кроме как выбирать из этого разнообразия, осуществляя таким образом на практике свою свободу.
Здесь в соответствии со схемой предыдущего параграфа рассматривается общая задача нелинейного программирования с гладкими функциями.
7.1. Постановка задачи.
Общей задачей нелинейной условной оптимизации мы будем называть условную задачу минимизации
где W выделяется как ограничениями типа равенств
так и ограничениями типа неравенств
(напомним, что неравенство означает покоординатные неравенства).
Нам также потребуется следующее обозначение: таким образом, если и если Для векторов операция «+» определяется покоординатно: Кроме того, через J ( x ) будет обозначаться множество индексов так называемых активных ограничений : это номера ограничений, которые в данной точке существенны. Например, на
Д о к а з а т е л ь с т в о. Возьмем r > 0 таким, чтобы где Для любого определим функцию равенством
З а д а ч а 7.1. Докажите, что в частности, покажите, что
| f n ( x n ) Ј f n ( x *), | (6) |
Отсюда, поскольку, как легко видеть,
Таким образом l 0 ** № 0. Положим теперь | м н о | m j **/ l 0 ** при j О J ( x *), Очевидно теперь, (10) выполняется автоматически, а (9) тривиально получается из (5). 7.5. Достаточные условия, существование, единственость. Ситуация с задачей (1)(3) несколько отличается от изучавшихся ранее, поскольку минимумы здесь могут быть двух типов. В случае, когда в точке минимума x * нет активных ограничений, ситуация полностью аналогична описанной в предыдущем параграфе, поскольку ограничения-неравенства в окрестности точки x * можно опустить (см. В случае же, когда минимум может достигаться на границе множества W и точка x * может не быть стационарной точкой (см. Мы ограничимся лишь формулировками результатов, поскольку в идейном плане они не доставляют ничего нового. Аналогом теоремы 6.9 может служить следующая Теорема (достаточные условия минимума). Пусть а допустимая точка такая, что для некоторых и одновременно не равных нулю, выполнены условия (9)(10) и при любых таких, что ( g ў j ( x *), h ) = 0 при j О J ( x *), m * j > 0; ( g ў j ( x *), h ) і 0 при j О J ( x *), m * j = 0 |
З а д а ч а 7.2. Докажите.
Что касается утверждений о существовании и единственности, то ситуация с результатами, которые могут быть доказаны изученными выше приемами, полностью аналогична.
З а д а ч а 7.3. Сформулируйте и докажите аналоги утверждений задач 6.7 и 6.8 для задачи (1)(3).
7.6. Об ограничениях-равенствах.
С целью упрощения изложения, начиная с этого момента, мы будем рассматривать задачу условной оптимизации, содержащую только ограничения-неравенства. Это, с одной стороны, не снижает общности изложения, поскольку ограничения-равенства сводятся к ограничениям-неравенствам: ограничение
С другой стороны, задачи с ограничениями-равенствами мы уже достаточно подробно рассматривали выше.
З а д а ч а 7.4. Докажите, что если функции выпуклы, то множество выпукло.
З а д а ч а 7.5. Докажите, что если функция выпукла, вместе с функцией то она аффинна:
7.7. Еще один достаточный признак условного минимума.
Напомним, что точка называется седловой точкой функции если при всех выполнены неравенства
Д о к а з а т е л ь с т в о. Пусть x произвольная допустимая точка, Тогда
Тогда из (12), поскольку а будет следовать нужное неравенство Для доказательства (13) заметим, что по условию теоремы
Равенство (13) вытекает теперь из (14), т.к. а
Тот факт, что доказанная теорема дает лишь достаточный признак условного минимума демонстрируетсмя в следующей задаче.
З а д а ч а 7.6. Покажите, что одномерная задача минимизации функции при ограничениях разрешима, но ее функция Лагранжа не имеет седловых точек.
З а д а ч а 7.7. Если в предыдущей теореме локальная седловая точка, то можно ли утверждать, что локальное решение задачи (Ответ: нельзя).
Перейдем к описанию методов решения задач с ограничениями-неравенствами. Многие из описываемых ниже методов либо существенно используют выпуклость объектов, фигурирующих в задаче, либо вообще неработоспособны на невыпуклых задачах.
7.8. Методы возможных направлений.
З а д а ч а 7.8*. Докажите, что если ( f 0 ( x ), z ) x в направлении z уменьшает значение функции f 0 (ср. с доказательством теоремы Ферма).
З а д а ч а 7.9*. Докажите, что если точка x допустима и ( g i ( x ), z ) i О J ( x ), то малое перемещение из точки x в направлении z не выводит из множества допустимых точек.
| ( f ў 0 ( x n ), z ) ® min, | (15) |
| ( g ў i ( x n ), z ) Ј 0, i О J ( x n ), | (16) |
Таким образом, если e мал ó и то ограничение в точке x почти обращается в равенство. В одном из вариантов метода возможных направлений выбирают последовательность и из очередной точки x n следующий шаг совершют в
где z n есть решение следующей линейной задачи
и нормализующими ограничениями (16). Подчеркнем, что в этой задаче неизвестными являются Длина шага в (18) выбирается таким образом, чтобы точка x n +1 не выходила из множества допустимых точек.
7.9. Методы проекции градиента.
Проекцией P W x точки x О R m на множество W М R m называется любая ближайшая к x точка множества W :
З а д а ч а 7.10. Докажите, что если W замкнуто и выпукло, то для любой точки проекция сужествует и единственна.
З а д а ч а 7.11. Приведите пример, когда проекция: а) не существует; б) не единственна.
В тех случаях, когда проекцию точки на множество допустимых точек задачи найти достаточно легко (например, когда линейное подпространство, полупространство, шар, R m + ) используют метод проекции градиента :
(см. рис. 26), являющийся прямым обобщением градиентного метода.
7.10. Методы линеаризации.
Суть этих методов, как следует из названия, состоит в линеаризации минимизируемой функции и ограничений в очередной точке x n строящейся релаксационной последовательности и объявлении следующим значением решения получающейся линейной задачи, задачи
Чтобы эта (линейная) задача была разрешима либо добавляют штраф в минимизируемую функцию, заменяя (19), например, задачей
либо добавляя к (20) простые ограничения, которые делают множество допустимых точек этой задачи ограниченным, например, (линейные) ограничения
Часто для уменьшения объема вычислительной работы среди ограничений (20) оставляют только
7.11. Методы штрафов.
Основная идея здесь заключается в переходе от задачи к задаче безусловной оптимизации, в которой «наказывается» либо удаление от множества W допустимых точек ( внешний штраф ), либо приближение изнутри множества W к его границе ( внутренний штраф ). Например, это можно сделать так. Для любого определим функцию равенством (индекс «out» станет понятен чуть ниже)
Сравнение геометрических интерпретаций задач и (23) изображено на рис. 28. З а д а ч а 7.13. Сформулируйте и докажите аналог задачи 7.5 для метода барьеров. З а д а ч а 7.14. Попытайтесь выписать аналоги штрафных функций и для общей задачи нелинейного программирования (1)(3), содержащей как ограничения-неравенства, так и ограничения-равенства. |
7.12. Двойственные методы.
Суть методов из этого весьма обширного класса в применении к задачам с ограничениями-неравенствами, так же как и в задачах с ограничениями-равенствами, заключается в замене условной задачи задачей поиска стационарной (часто седловой) точки функции Лагранжа. В выпуклом случае задача и задача о поиске седловой точки функции Лагранжа в силе теоремы Таккера эквивалентны. Например, применение простейшего (градиентного) метода к последней задаче приводит к следующему методу Удзавы :
Для поиска седловой точки в двойственных методах применяют почти весь спектр описанных выше методов методы Ньютона, квазиньютоновские методы, методы сопряженных направлений
File based on translation from T E X by T T H, version 3.05.
Created 10 Jun 2001, 20:58.