какое наибольшее количество целых чисел

Какие числа называются целыми

Определение целых чисел

Что важно знать о целых числах:

Целые числа на числовой оси выглядят так:

На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.

В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.

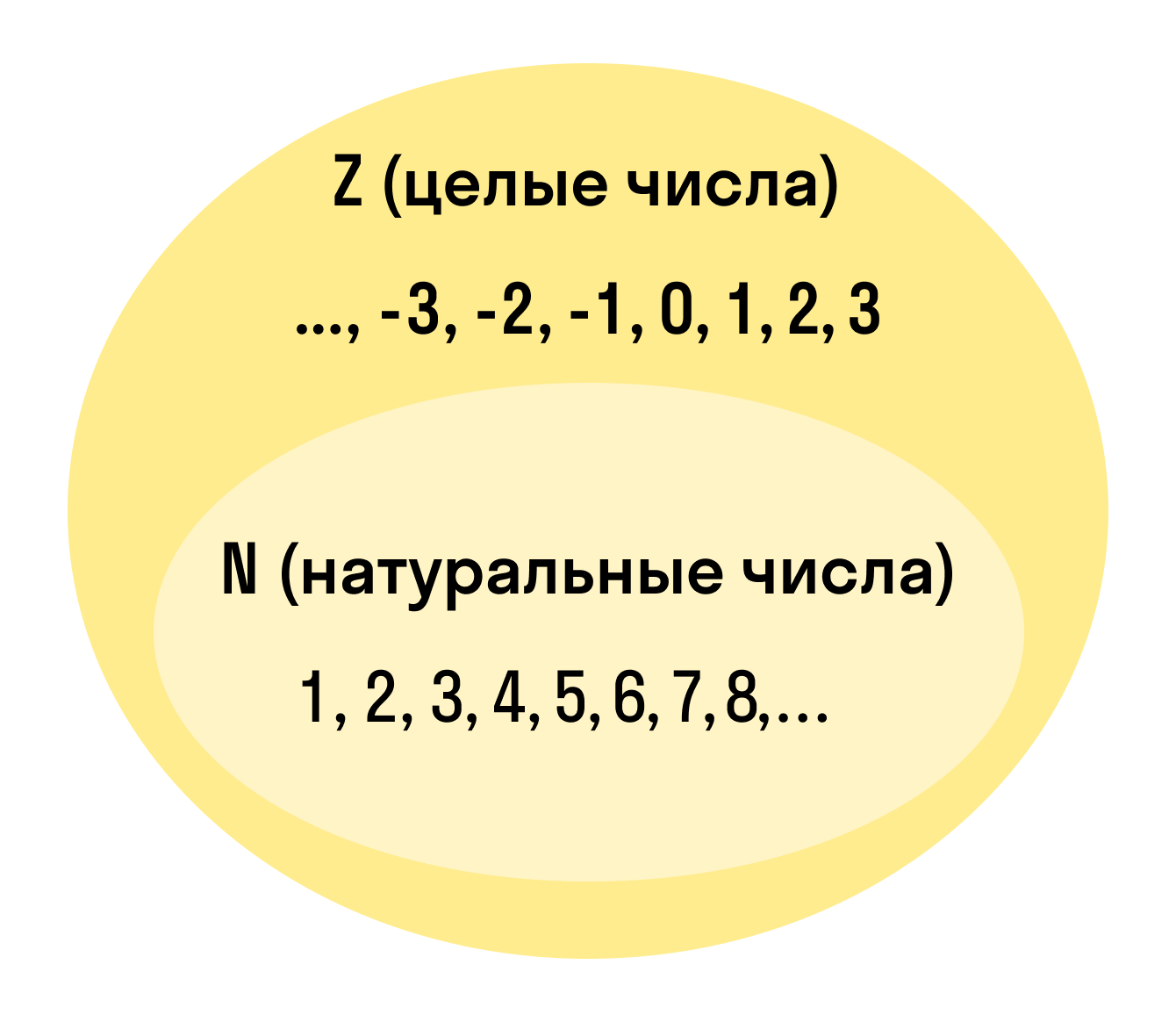
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.

Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.

Выглядит эти ребята вот так:

Последовательность целых чисел можно записать так:

Свойства целых чисел

Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:

Источник

Какое наибольшее количество целых чисел

Отношение трёхзначного натурального числа к сумме его цифр — целое число.

а) Может ли это отношение быть равным 11?

б) Может ли это отношение быть равным 5?

в) Какое наибольшее значение может принимать это отношение, если число не делится на 100 и его первая цифра равна 7?

Пусть это число состоит из цифр a, b, c, тогда оно равно 100a + 10b + c.

При равенство будет выполнено. Следовательно, 198 — один из возможных примеров.

Но следовательно, левая часть равенства не меньше 95, а правая часть не больше 36. Противоречие.

в) Число имеет вид 700 + 10b + c, необходимо найти наибольшее целое значение выражения Разберем случаи, когда b + c ≤ 2 (см. табл.). Для таких b и c наибольшее отношение равно 80.

b	c
0	1
0	2
1	0
1	1
2	0

При b + c ≥ 3 справедлива оценка

поэтому в этом случае наибольшее возможное отношение меньше 80. Следовательно, наибольшее возможное отношение достигается при b = 2, c = 0, оно равно 80.

Ответ: а) да, б) нет, в) 80.

Приведём решение пункта б) Дьяковой Дарьи (Москва).

Положим и запишем условие в виде По условию, S натуральное, а значит, число должно заканчиваться либо на 0, либо на 5. Наименьшее возможное значение S соответствует наименьшему поэтому С другой стороны, Полученное противоречие показывает, что среди трехзначных чисел, оканчивающихся нулем, искомого нет.

Рассмотрим числа оканчивающиеся на 5. В этом случае С другой стороны, Выпишем трехзначные числа, заканчивающиеся на 5, сумма цифр которых не меньше 21 и не больше 23. Получим числа: 995, 985, 975, 895, 885, 795. Но каждое из найденных чисел при делении на 5 даст больше 23. Следовательно, среди трехзначных чисел, оканчивающихся на 5, искомого тоже нет.

Пример числа, удовлетворяющего требованиям пункта а), единственный. Действительно, при левая часть равенства не меньше 89. А правая часть при не больше 79, при не меньше 90.

Другие пути решения аналогичных задач показаны нами в заданиях 563580 и 563695.

Аналоги к заданию № 563580: 563677 563659 Все

Источник

Какое наибольшее количество целых чисел

На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Пусть среди написанных чисел k положительных, l отрицательных и m нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому

а) Заметим, что в левой части каждое слагаемое делится на 9, поэтому — количество целых чисел — делится на 9. По условию поэтому

Таким образом, написано 36 чисел.

б) Приведём равенство к виду

Так как получаем, что откуда Следовательно, отрицательных чисел больше, чем положительных.

в) (оценка) Подставим в правую часть равенства

Так как получаем:

;

то есть положительных чисел не более 16.

в) (пример) Приведём пример, когда положительных чисел ровно 16. Пусть на доске 16 раз написано число 9, 18 раз написано число −18 и два раза написан 0.

указанный набор удовлетворяет всем условиям задачи.

Источник

Готовимся к олимпиаде. Задачи на ЧЁТНОСТЬ.

Ищем педагогов в команду «Инфоурок»

ЧЁТНЫЕ И НЕЧЁТНЫЕ ЧИСЛА

Легко доказать или показать на примерах следующие свойства чётности для целых чисел:

Сумма чётных чисел чётна.

Сумма двух нечётных чисел чётна.

Сумма чётного и нечётного чисел нечётна.

Произведение любого числа на чётное – чётно.

Если произведение нечётно, то все сомножители нечётны.

Сумма чётного количества нечётных чисел чётна.

Сумма нечётного количества нечётных чисел нечётна.

Разность и сумма двух данных чисел – числа одной чётности.

Если объекты можно разбить на пары, то их количество чётно.

Кузнецу заказали выковать десять мечей. Каждый меч может стоить 3, 5 или 7 златников. Могут ли они стоить вместе 53 златника?

Сумма чётного количества нечётных чисел чётна. У нас есть 10 мечей, цена каждого меча – нечётное число, значит, их сумма должна быть чётна. Но 53 – число нечётное, поэтому получить его в виде суммы 10 нечётных чисел нельзя.

Можно ли 7 селений соединить между собой попарно так, чтобы каждое было соединено напрямую ровно с тремя другими?

Если мы рассматриваем объекты типа верёвки – провода, дороги, рукопожатия, знакомства и т.д., то при любом количестве объектов число концов должно быть чётным. Предположим, что мы соединили между собой 7 селений попарно так, чтобы каждое было соединено ровно с тремя другими. Подсчитаем количество концов дорог, соединяющих эти селения. Понятно, что их число должно быть чётным. От каждого из 7 селений отходит 3 конца дорог, всего 7 ∙ 3 = 21 конец, число нечётное. Значит, нельзя 7 селений соединить между собой попарно так, чтобы каждое было соединено ровно с тремя другими.

13 команд мечников участвуют в королевском однокруговом турнире. Докажите, что в любой момент есть команда, сыгравшая чётное число встреч. (Однокруговой турнир – когда каждая команда играет с каждой ровно один раз).

Подсчитаем, сколько встреч провела каждая команда, и просуммируем полученные числа. В общей сумме каждая игра учитывается два раза. Если же подсчитать сумму игр 13 команд, сыгравших по нечётному числу встреч, результат будет нечётный. Чтобы общая сумма игр получилась чётной, хотя бы одна команда должна сыграть чётное число встреч.

В секции фехтования мальчиков в 14 раз больше, чем девочек, при этом всего в секции не более 20 человек. Смогут ли они разбиться на пары?

Пусть количество девочек х, тогда мальчиков 14х, всего 15х. Но 15х 20, значит, х = 1. Мальчиков 14, девочек – 1, всего 15 человек. Но 15 человек нельзя разбить на пары.

ЧЁТНОСТЬ КАК ИНВАРИАНТ

Инвариант – термин, обозначающий нечто неизменяемое. Разберём несколько задач, где не меняется чётность некоторой величины.

Казначей положил на стол 6 монет, одну из них вверх орлом, другие – решкой. Можно ли все монеты положить вверх орлом, если разрешено одновременно переворачивать две монеты?

При переворачивании двух монет одновременно четность числа монет, лежащих орлом вверх, не меняется. Докажем это.

Если перевернуть две монеты вверх орлом, то они станут вверх решкой (ОО → РР). Орлов стало на два меньше, а решек – на два больше, чётность не изменится.

Если перевернуть две монеты вверх решкой, то они станут вверх орлом (РР → ОО). Орлов стало на два больше, а решек – на два меньше, чётность не изменится.

Если перевернуть одну монету вверх орлом, а другую – вверх решкой (ОР → РО), количество орлов, как и количество решек, останется прежним. Чётность не изменится.

В любом случае чётность числа монет, лежащих вверх орлом, не изменится. Если сначала вверх орлом лежала одна монета (а 1 – число нечётное), значит, при любой манипуляции количество таких монет может быть только нечётным, и соответственно, все 6 монет положить вверх орлом не удастся.

Можно ли в таблице 5 х 5 расставить 25 натуральных чисел так, чтобы во всех строках суммы были чётные, а во всех столбцах – нечётные?

Сложим все полученные суммы по строкам: 25 чётных сумм вместе дают чётное число.

Сложим все полученные суммы по столбцам: 25 нечётных сумм вместе дают нечётное число.

Но сумма чисел во всех строках (в нашем примере чётное число) должна быть равна сумме чисел во всех столбцах (в нашем примере нечётное число), что невыполнимо в нашем примере.

В таблице 6 х 6 за один ход можно поменять все знаки в любой строке или в любом столбце на противоположные. Можно ли таким образом из таблицы, приведённой:

а) Рассмотрим. Как меняется количество минусов за один ход. Допустим, мы меняем знаки в строчке. Заметим, что при этом количество минусов в других строчках остается неизменным. Если в изменяемой строчке было чётное количество минусов, то было и чётное количество плюсов, и после смены знаков чётность общего числа минусов в таблице не изменится.

Если там было нечётное количество минусов, то было и нечётное количество плюсов, и после смены знаков чётность общего числа минусов в таблице тоже не изменится.

Аналогично для столбца. Значит, если вначале было 17 минусов (нечётное число), то получить таблицу из 36 минусов (чётное число) нельзя, так как минусов всегда будет нечётное количество.

б) во второй таблице число минусов чётное, но получить нужную таблицу все равно нельзя.

Рассмотрим квадрат 2 х 2 в правом верхнем углу таблицы. Количество минусов в этом отдельно взятом кусочке меняется по тем же правилам, что и во всей таблице, причём чётность количества минусов в этой табличке 2 х 2 тоже не меняется – остаётся нечётной. Значит, даже в этом кусочке нельзя получить все 4 минуса, т.е. будет присутствовать хотя бы один плюс.

Ответ : а) нет; б) нет.

На столе стоят 16 кубков, один из них вверх дном. Можно ли все кубки поставить правильно, если можно одновременно переворачивать по 4 кубка?

Вначале правильно стоят 15 кубков (нечётное число), а вверх дном 1 кубок (нечётное число).

Пусть мы переворачиваем все 4 кубка вверх дном. Тогда «нечёт» – 4 = «нечёт» число кубков будут стоять правильно.

Теперь переворачиваем 3 кубка вверх дном, а 1 кубок – становится правильно. Т.е. 3 кубка, стоящих правильно, будут теперь перевёрнуты, а тот кубок, который был изначально перевёрнут, будет тоже стоять правильно.

Тогда «нечёт» – 3 + 1 = «нечёт» число кубков будут стоять правильно.

Переворачиваем 2 кубка вверх дном и два кубка – станут стоять правильно. Тогда «нечёт» + 2 = «нечёт» число кубков будут стоять правильно.

Если перевернём 1 кубок вверх дном и 3 установим правильно, то получим опять «нечёт» – 1 + 3 = «нечёт» число кубков будут стоять правильно.

Если все 4 кубка установим правильно, то «нечёт» + 4 = «нечёт» число кубков будут стоять правильно.

Итак, чётность правильно стоящих кубков при переворачивании не меняется, то есть остаётся нечётным на любом шаге. Значит, установить все 16 кубков правильно невозможно.

ЧЁТНОСТЬ СУММЫ И ПРОИЗВЕДЕНИЯ ЧИСЕЛ

На доске написаны числа 1, 2, 3, …, 2017, 2018. Разрешается стереть с доски любые два числа и вместо них записать модуль их разности. В конце концов на доске останется одно число. Может ли оно равняться нулю?

Вычислим сначала сумму всех чисел, записанных на доске. Она равна:

1 + 2 + 3 + … + 2016 + 2017 + 2018 = (1 + 2018) + (2 + 2017) + … + (1008 + 1009) = [всего 1009 пар] = 2019 ∙ 1009 = нечётное число (так как произведение нечётных чисел равно нечётному числу).

Теперь посмотрим, как меняется эта сумма, если из неё взять два слагаемых и заменить их разностью этих чисел.

Если оба числа чётные, то их сумма была чётной, и их разность тоже будет чётной. Сумма всех данных чисел уменьшится на чётное число, то есть

Чётность суммы всех данных чисел не изменится.

Если оба числа нечётные, то их сумма была чётной, и их разность тоже будет чётной. Сумма всех данных чисел уменьшится на чётное число, то есть

Чётность суммы всех данных чисел не изменится.

Если одно число чётное, а другое нечётное, то их сумма была нечётной, и их разность тоже будет нечётной. Чётность общей суммы всех данных чисел не изменится.

Значит, у нас могут получаться только нечётные суммы всех записанных чисел на любом шаге, а нуль – число чётное, и оно в конце на доске остаться не может.

Например: 1 2 – 2 2 – 3 2 + 4 2 + 5 2 – 6 2 – 7 2 + 8 2 + 9 2 – 10 2 – 11 2 + 12 2 = 12.

б) Докажем, что это невозможно.

Квадраты чётных чисел – чётные числа, а квадраты нечётных чисел – нечётные числа. Среди 70 последовательных чисел ровно половина – нечётные, то есть в данной алгебраической сумме 35 нечётных чисел и 35 чётных, значит, их сумма всегда нечётна, и, следовательно, не может быть равна 0.

На доске написаны последовательные натуральные числа от 1 до 2015. Разрешается за одну операцию стереть любые два числа и вместо них поставить их произведение. Какое наибольшее число операций можно сделать, прежде чем все числа на доске станут чётными? Какое наименьшее?

Произведение двух нечётных чисел – нечётное, а произведение любого натурального числа на чётное – чётное. Посчитаем, какое наибольшее число операций можно сделать, прежде чем все числа на доске станут чётными.

Оставим на доске одно из нечётных чисел и не будем его трогать, пока есть другие числа. Тогда только после последней операции не останется нечётных чисел. Сколько же таких операций будет проведено?

За каждую операцию количество чисел уменьшается на одно (так как вместо двух чисел записывается одно). Значит, наибольшее возможное число операций 2015 – 1 = 2014.

Посчитаем, какое наименьшее число операций можно сделать, прежде чем все числа на доске станут чётными.

Каждой операцией мы можем убрать не более чем одно число, в том числе и нечётное.

Всего нечётных чисел на доске + 1 = 1007 + 1 = 1008. Значит, нужно хотя бы 1008 операций.

Как можно действовать, чтобы за 1008 операций все числа на доске стали чётными: каждым ходом умножать одно из оставшихся нечётных чисел на чётное, тогда вместо них будет появляться их чётное произведение, и ровно за 1008 операций все числа на доске станут чётными.

Источник

Какое наибольшее количество целых чисел

БАЗА ЗАДАНИЙ

Задание № 18. Задачи на логику.

54. Верно ли, что для любого набора положительных чисел, каждое из которых не превосходит 11, а сумма которых больше 110, всегда можно выбрать несколько чисел так, чтобы их сумма была не больше 110, но больше:
а) 99;
б) 101;
в) 100.
Ответ: а) да; б) нет; в) да

55. а) Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа.
б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа?
в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа.
Ответ: а) пример: 2529; б) нет; в) 8655 и все его перестановки

а) Приведите пример такой последовательности, состоящей из четырех членов, сумма которых равна 50.
б) Может ли такая последовательность состоять из 6 членов и содержать два одинаковых числа?
в) Какое наименьшее значение может принимать сумма членов такой последовательности при n=10?
Ответ: а) пример: 1, 12, 17, 20; б) да; в) 70

58. Рассмотрим частное трехзначного числа, в записи которого нет нулей, и произведения его цифр.
а) Приведите пример числа, для которого это частное равно 113/27.
б) Может ли это частное равняться 125/27?
в) Какое наибольшее значение может принимать это частное, если оно равно несократимой дроби со знаменателем 27?
Ответ: а) пример: 339; б) нет; в) 931/27

59. На доске написано 30 чисел: десять «5», десять «4» и десять «3». Эти числа разбивают на 2 группы, в каждой их которых есть хотя-бы одно число. Среднее арифметическое чисел в первой группе равно А, среднее арифметическое во второй группе равно В.
а) Приведите пример разбиения исходный чисел на 2 группы, при котором среднее арифметическое всех чисел меньше (А+В)/2.
б) Докажите, что если разбить исходные числа на 2 группы по 15 чисел, то среднее арифметическое всех чисел будет равно (А+В)/2.
в) Найдите наибольшее возможное значение выражения (А+В)/2.
Ответ: а) пример: в первой группе все пятерки, во второй все четверки и тройки; в) 4 14 /₂₉

60. На доске написано число 2045 и еще несколько (не менее двух) натуральных чисел, не превосходящих 5000. Все написанные на доске числа различны. Сумма любых двух из написанных чисел делится на какое-нибудь из остальных.
а) Может ли на доске быть написано ровно 1024 числа?
б) Может ли на доске быть написано ровно пять чисел?
в) Какое наименьшее количество чисел может быть написано на доске?
Ответ: а) да; б) да; в) 4

61. В нескольких одинаковых бочках налито некоторое количество литров воды (необязательно одинаковое). За один раз можно перелить любое количество воды из одной бочки в другую.
а) Пусть есть четыре бочки, в которых 29, 32, 40, 91 литров. Можно ли не более чем за четыре переливания уравнять количество воды в бочках?
б) Путь есть семь бочек. Всегда ли можно уравнять количество воды во всех бочках не более чем за пять переливаний?
в) За какое наименьшее количество переливаний можно заведомо уравнять количество воды в 26 бочках?
Ответ: а) да; б) нет; в) 25

62. Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 12 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кино­фильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое пяти оставшихся оценок.
а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться 1/25?
б) Может ли эта разность рейтингов, вычисленных по старой и новой системам оценивания, равняться 1/35?
в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Ответ: а) нет; б) да; в) 6/7

63. На сайте проводится опрос, кого из 134 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста – доля голосов, отдан­ных за него, в процентах, округленная до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно.
а) Всего проголосовало 17 посетителей сайта, и рейтинг первого футболиста стал равен 41. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста?
б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшится не менее, чем на 27?
в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Ответ: а) 39; б) да; в) 167

64. а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?
б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?
в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.
Ответ: а) да; б) нет; в) 110

65. В группе поровну юношей и девушек. Юноши отправляют электронные письма девушкам. Каждый юноша отправляет или 4 письма, или 21 письмо, причем и тех, и других юношей было не менее двух. Возможно, что какой-то юноша отправил какой-то девушке несколько писем.
а) Могло ли оказаться так, что каждая девушка получила ровно 7 писем?
б) Какое наименьшее количество девушек могло быть в группе, если известно, что все они получили писем поровну?
в) Пусть все девушки получили различное количество писем (возможно какая-то девушка не получила писем вообще). Каково наибольшее возможное количество девушек в такой группе?
Ответ: а) да; б) 17; в) 41

67. На окружности некоторым способом расставили натуральные числа от 1 до 21 (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.
а) Могли ли все полученные разности быть не меньше 11?
б) Могли ли все полученные разности быть не меньше 10?
в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа k можно так расставить числа, чтобы все разности были не меньше k?
Ответ: а) нет; б) да; в) 6

69. Даны n различных натуральных чисел, составляющих арифметическую прогрессию (n ≥ 3).
а) Может ли сумма всех данных чисел быть равной 18?
б) Каково наибольшее значение n, если сумма всех данных чисел меньше 800?
в) Найдите все возможные значения n, если сумма всех данных чисел равна 111?
Ответ: а) да; б) 39; в) 3 или 6

70. Имеются каменные глыбы: 50 штук по 800 кг, 60 штук по 1 000 кг и 60 штук по 1 500 кг (раскалывать глыбы нельзя).
а) Можно ли увезти все эти глыбы одновременно на 60 грузовиках, грузоподъёмностью 5 тонн каждый, предполагая, что в грузовик выбранные глыбы поместятся?
б) Можно ли увезти все эти глыбы одновременно на 38 грузовиках, грузоподъёмностью 5 тонн каждый, предполагая, что в грузовик выбранные глыбы поместятся?
в) Какое наименьшее количество грузовиков, грузоподъёмностью 5 тонн каждый, понадобится, чтобы вывезти все эти глыбы одновременно, предполагая, что в грузовик выбранные глыбы поместятся?
Ответ: а) да; б) нет; в) 39

71. Последовательность цифр устроена следующим образом. Две первые цифры a и b заданы заранее и не равны нулю. Справа к ним приписываются цифры произведения ab. Затем справа приписываются цифры числа, полученного произведением последних двух цифр, и так далее. Например, если первые две цифры были a=6 и b=7, то получается последовательность
6, 7, 4, 2, 8, 1, 6,…
а) Приведите пример такой последовательности, в которой шесть первых членов отличны от нуля, а все члены начиная с седьмого равны нулю.
б) Докажите, что любая последовательность, построенная таким образом, с какого-то момента становится периодической (цифры начинают повторяться в одном и том же порядке).
Ответ: а) 1, 5, 5, 2, 5, 1, 0, 0, …

72. Будем называть четырёхзначное число очень счастливым, если все цифры в его десятичной записи различны, а сумма первых двух из этих цифр равна сумме последних двух из них. Например, очень счастливым является число 3140.
а) Существуют ли одиннадцать последовательных четырёхзначных чисел, среди которых ровно два очень счастливых?
б) Может ли разность двух очень счастливых четырёхзначных чисел равняться 2017?
в) Найдите наименьшее простое число, для которого не существует кратного ему очень счастливого четырёхзначного числа.
Ответ: а) да, например, 5023, 5024, …, 5033; б) нет; в) 11.

73. Вася и Петя решали задачи из сборника, причем каждый следующий день Вася решал на одну задачу больше, чем в предыдущий, а Петя — на две задачи больше, чем в предыдущий день. В первый день каждый решил хотя бы одну задачу, а в итоге каждый решил все задачи сборника.

а) Могло ли быть в сборнике 85 задач?

б) Могло ли быть в сборнике 213 задач, если каждый из мальчиков решал их более трех дней?

в) Какое наибольшее количество дней мог решать задачи Петя, если Вася решил весь сборник за 16 дней, а количество задач в сборнике меньше 300.

Ответ: а) да, б) нет, в) 14.

74. Есть синие и красные карточки. Всего карточек 50 штук. На каждой написаны натуральные числа, среднее арифметическое которых равно 16. Все числа на синих карточках разные. При этом любое число на синей карточке больше, чем любое на красной. Числа на синих увеличили в 2 раза, после чего среднее арифметическое стало равно 31,2.

а) Может ли быть 10 синих карточек?
б) Может ли быть 10 красных карточек?
в) Какое наибольшее количество синих карточек может быть.
Ответ: а) да, б) нет, в) 35.

75. Последовательность натуральных чисел (a _n ) состоит из 400 членов. Каждый член последовательности, начиная со второго, либо вдвое больше предыдущего, либо на 98 меньше предыдущего.

а) Может ли последовательность (a_n) содержать ровно 5 различных чисел?

б) Чему может равняться a₁, если a₁₀₀ =75?
в) Какое наименьшее значение может принимать наибольший член последовательности (a_n)?

Ответ: а) да, б) 9777, в) 112.

76. Пять различных натуральных чисел таковы, что никакие два не имеют общего делителя, больше 1.

а) Может ли сумма всех пяти чисел быть равна 26?
б) Может ли сумма всех пяти чисел быть равна 23?
в) Какое наименьшее значение может принимать сумма всех пяти чисел?
Ответ: а) Да; б) Нет; в) 18.

77. В ящике лежат 95 фруктов, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два фрукта различной массы, а средняя масса всех фруктов равна 100 г. Средняя масса фруктов, масса каждого из которых меньше 100 г, равна 73 г. Средняя масса фруктов, масса каждого из которых больше 100 г, равна 115 г.
а) Могло ли в ящике оказаться поровну фруктов массой меньше 100 г и фруктов массой больше 100 г?
б) Могло ли в ящике оказаться меньше 10 фруктов, масса каждого из которых равна 100 г?
в) Какую наибольшую массу может иметь фрукт в этом ящике?

Ответ: а) нет; б) нет; в) 857

78. В течении n дней каждый день на доску записывают натуральные числа, каждые из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество чисел меньше, чем в предыдущий день.
а) Известно, что сумма чисел, записанных в первый день, равна 7. Может ли n быть больше 6?
б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 2, среднее арифметическое всех чисел, записанных за все дни, быть больше 2,5?
в) Известно, что n=6. Какое наименьшее количество чисел могло быть записано за все эти дни?

Источник