какое движение считают переносным а какое относительным
Относительное, переносное и абсолютное движения точки
Сложное (составное) движение точки – такое движение, при котором точка одновременно участвует в двух или нескольких видах движения. Например, пассажир, перемещающийся в вагоне движущегося поезда или на палубе плывущего корабля по отношению к условно неподвижной системе отсчета, связанной с землей, совершает сложное движение.
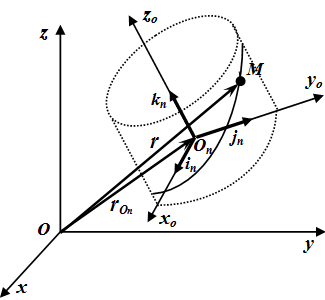
Рассмотрим движущееся тело А и точку М, не принадлежащую этому телу, а совершающую по отношению к нему некоторое движение (рис. 3.40). Выберем две системы координат: неподвижную систему координат О1х1 y1 z1 в условно неподвижной системе отсчета и систему координат Оху z, которая проведена через некоторую точку тела О и жестко с ним связана. Систему Оху z называют подвижной системой координат.




Рис. 3.40 абсолютной скоростью и
абсолютным ускорением.
Движение точки М по отношению к подвижной системе координат Оху z называется относительным движением и определяется радиус-вектором 
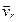

Движение подвижной системы координат относительно неподвижной называется переносным. Точки тела А, связанного с подвижной системой отсчета, имеют различные скорости и ускорения, в зависимости от вида движения твердого тела (см. п. 3).
Движение точки О подвижной системы координат относительно точки О1 неподвижной системы определяется радиус–вектором 

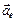
Положение точки М относительно подвижной системы отсчета (рис. 3.40) определяется радиусом вектором


Положение точки М по отношению к неподвижной системе отсчета можно определить радиус-вектором
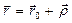
Основной задачей при изучении сложного движения точки является установление зависимостей между скоростями и ускорениями абсолютного, относительного и переносного движений.
Последнее изменение этой страницы: 2019-04-09; Просмотров: 254; Нарушение авторского права страницы
Абсолютная, относительная и переносная скорости
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
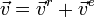
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
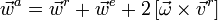
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость 
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Переносное движение
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
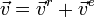
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
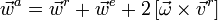
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость 
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Переносное движение» в других словарях:
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — в механике, движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной). (см. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор… … Физическая энциклопедия
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — перемещение подвижной системы отсчёта (напр. движение вагона с передвигающимся в нём человеком), по отношению к которой точка, тело (человек) совершает относительное (см.) … Большая политехническая энциклопедия
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — перемещение подвижной системы отсчета, по отношению к которой точка или тело совершает относительное движение … Большой Энциклопедический словарь
переносное движение — Движение подвижной системы отсчета по отношению к основной системе отсчета. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика … Справочник технического переводчика
переносное движение — 3.29 переносное движение : Совместное движение сооружения и основания во время землетрясения как единого недеформируемого целого с ускорениями (скоростями или смещениями) основания. Источник: СП 14.13330.2014: Строительство в сейсмических районах … Словарь-справочник терминов нормативно-технической документации
переносное движение — движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной). * * * ПЕРЕНОСНОЕ ДВИЖЕНИЕ ПЕРЕНОСНОЕ ДВИЖЕНИЕ, перемещение подвижной системы отсчета, по отношению к которой точка или тело… … Энциклопедический словарь
переносное движение — nešamasis judėjimas statusas T sritis fizika atitikmenys: angl. bulk motion vok. Führungsbewegung, f rus. переносное движение, n pranc. mouvement d’entraînement, m; mouvement translatif, m … Fizikos terminų žodynas
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — движение подвижной системы отсчёта по отношению к т. н. абсолютной (обычно инерциальной) системе отсчёта (см. Относительное движение) … Большой энциклопедический политехнический словарь
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной) … Естествознание. Энциклопедический словарь
переносное движение — Движение подвижной системы отсчёта по отношению к основной системе отсчёта … Политехнический терминологический толковый словарь
Какое движение считают переносным а какое относительным
Все в природе движется. Любое тело, которое мы условно считаем неподвижным, в действительности движется. Одно какое-либо движение накладывается на другое движение. Поэтому весьма важно знать, как складываются движения, как складываются скорости и ускорения какого-либо тела, которое одновременно участвует в нескольких движениях. Чтобы разобраться в этом вопросе, прежде всего введем представление о так называемом абсолютном (в условном смысле) движении, о переносном и относительном движениях.
Одно и то же движение представляется нам происходящим по-разному в зависимости от способа его наблюдения. Когда на железнодорожной станции один из двух стоящих рядом поездов приходит в движение, то пассажирам другого, неподвижного, поезда кажется, что пошел их поезд. Конечно, достаточно бывает бросить взгляд на платформу станции, чтобы эта иллюзия исчезла. Станционные постройки в этом случае играют роль основной системы ориентировки.
Если бы ход поездов был совершенно плавен и станционные постройки, например вследствие тумана, не были видны, то, наблюдая движение освещенных окон поезда, пассажиры обоих поездов могли бы судить о движении поездов по отношению друг к другу, но не в состоянии были бы решить вопрос, какой из поездов пошел, а какой неподвижен.
Если бы мы представили себе двух наблюдателей, замечающих, что они удаляются друг от друга, и находящихся где-то в космическом пространстве, где почему-либо не видны звезды или какие-либо предметы, позволяющие наблюдателям каким-либо образом ориентироваться в характере их движения, то вопрос о том, какой из наблюдателей покоится, а какой движется, для них утратил бы смысл. Каждый из них вправе был бы считать себя покоящимся, а другого движущимся.
Таким образом, очевидно, что с кинематической точки зрения, т. е. если отвлечься от причин, вызывающих движение, всякое движение следует рассматривать как относительное. С этой кинематической точки зрения все системы ориентировки являются равноправными; любую из них мы можем при данном исследовании интересующих нас движений условно считать неподвижной; такую условно неподвижную систему ориентировки мы будем называть основной системой ориентировки. Движение относительно основной системы ориентировки называют абсолютным движением.
В приведенном примере с двумя поездами с кинематической точки зрения не является обязательным, чтобы в качестве основной системы непременно были избраны станционные постройки. Пассажир движущегося поезда имеет право предпочесть систему ориентировки, связанную с его поездом; считая ее основной, он будет «кажущееся» движение станционных построек именовать абсолютным движением.
Всякую систему ориентировки, которая совершает какое-либо движение относительно основной системы, мы будем называть подвижной системой ориентировки. Движение относительно подвижной системы ориентировки называют относительным движением, а движение самой подвижной системы ориентировки называют переносным движением. Так, например, если в вышеупомянутом случае двух поездов в качестве основной системы ориентировки избраны станционные постройки, то система ориентировки, связанная с движущимся поездом, будет представлять собой подвижную систему ориентировки; движение поезда и пассажиров, сидящих в нем на своих местах, является переносным движением; прогулка какого-либо пассажира по коридору вагона, наблюдаемая другими пассажирами вагона, сидящими на своих местах, есть относительное движение; та же прогулка пассажира по коридору движущегося вагона, наблюдаемая с платформы вокзала, представляет собой абсолютное движение.
Представим себе, что материальная точка движется в подвижной системе. Обозначим через 


Под абсолютной скоростью 


Скорость абсолютного движения равна геометрической сумме скоростей переносного и относительного движений:
Это утверждение, высказанное с полной ясностью еще Галилеем, называют галилеееым законом сложения скоростей. В простейших случаях, в особенности когда все три скорости направлены по одной прямой и неизменны во времени, галилеев закон сложения скоростей представляется как бы самоочевидным и сознательно или бессознательно применяется всеми в оценке движений, встречающихся в обыденной жизни. Например, каждый знает, что, плывя в лодке вниз по течению, мы движемся быстрее, чем в неподвижной воде, на величину «быстроты» течения воды.
Сложное движение точки. Теорема Кориолиса
Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.
Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.
Сложное (составное) движение точки
Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.
Такое движение точки называется сложным или составным.
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).
Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.
Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.
Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.
Относительная скорость и ускорение
Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.
Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.
Переносная скорость и ускорение
Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.
Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.
Подставляем в (4):
.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.
Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.
Абсолютная скорость и ускорение
Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.
Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.
Теорема о сложении скоростей
При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Доказательство
Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.
Теорема Кориолиса о сложении ускорений
При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.
Доказательство
В последнем члене применим (6) и (2).
.
Тогда
.

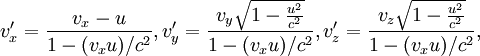


Warning: Use of undefined constant expert_review_likes - assumed 'expert_review_likes' (this will throw an Error in a future version of PHP) in /var/www/www-ars1963/data/www/ck62.ru/wp-content/themes/colormag/comments.php on line 93